题目内容
9.在矩形ABCD中,AB=2,AD=3,点P在边AD上,连接BP,点A关于直线BP的对称点为A1
(1)点A1落在BC边上,求AP的长;
(2)点A1落在线段PC上,求AP的长;
(3)点A1到直线CD的距离等于A1B的长,求AP的长.
分析 (1)如图1中,只要证明AB=AP即可解决问题.
(2)如图2中,先证明CP=CB,利用勾股定理求出PD,即可解决问题.
(3)如图3中,点A1到直线CD的距离等于A1B的长时,过点A1作EF⊥AD垂足为E,交BC于F.先证明∠BA1F=30°,由此即可解决问题.
解答 解:(1)如图1中,
∵点A1落在BC边上,
∴∠ABP=∠PBA1=45°,
∵四边形ABCD是矩形,
∴∠A=90°,
∴∠ABP=∠APB=45°,
∴AP=AB=2.
(2)如图2中,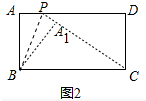
∵点A1落在线段PC上,
∴∠APB=∠BPA1,
∵AD∥BC,
∴∠APB=∠PBC,
∴∠CPB=∠CBP,
∴CP=CB=3,
在Rt△PDC中,PD=$\sqrt{P{C}^{2}-C{D}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∴PA=AD-PD=3-$\sqrt{5}$.
(3)如图3中,点A1到直线CD的距离等于A1B的长时,过点A1作EF⊥AD垂足为E,交BC于F.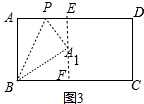
在Rt△BFA1中,BF=1,BA1=2,
∴sin∠BA1F=$\frac{1}{2}$,
∴∠BA1F=30°,A1F=$\sqrt{3}$,EA1=2-$\sqrt{3}$,
在Rt△A1PE中,∠PA1E=60°,
∴∠A1PE=30°,
∴PE=$\sqrt{3}$EA1=2$\sqrt{3}$-3,
∴AP=1-(2$\sqrt{3}$-3)=4-2$\sqrt{3}$.
点评 本题考查轴对称的性质、矩形的性质、勾股定理等知识,解题的关键是利用翻折不变性解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.我校开展的“we can微阅读”读书活动,为了解七年级480名学生读书情况,随机查了七年级50名学生读书的册数,统计数据如表所示:
则全校七年级学生的读书册数等于3册的人数( )
| 册数 | 0 | 1 | 2 | 3 | 4册及以上 |
| 人数 | 3 | 13 | 16 | a | 5 |
| A. | 13 | B. | 16 | C. | 104 | D. | 128 |
14.若a:b=1:2,b:c=4:6,则a:b:c=( )
| A. | 1:2:3 | B. | 1:2:4 | C. | 1:2:6 | D. | 1:4:6 |
18.在1、-2、3这三个数中,任选两个数的积作为k的值,使反比例函数y=$\frac{k}{x}$的图象在第二、四象限的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{9}$ |
 如图,圆的直径为20cm,BC过圆心O,且AO是三角形ABC的高,求三角形ABC的面积.
如图,圆的直径为20cm,BC过圆心O,且AO是三角形ABC的高,求三角形ABC的面积.