题目内容
12.阅读理解题:解不等式(x+1)(x-3)>0.解:根据两数相乘,同号得正,原不等式可以转化为:
$\left\{\begin{array}{l}{x+1>0}\\{x-3>0}\end{array}\right.$或$\left\{\begin{array}{l}{x+1<0}\\{x-3<0}\end{array}\right.$,
解不等式组$\left\{\begin{array}{l}{x+1>0}\\{x-3>0}\end{array}\right.$,得x>3;
解不等式组$\left\{\begin{array}{l}{x+1<0}\\{x-3<0}\end{array}\right.$,得x<-1,
所以原不等式的解集为x>3或x<-1.
问题解决:根据以上阅读材料,解不等式(2x-3)(1+3x)<0.
分析 由两数相乘异号得负得出关于x的不等式组,解之可得答案.
解答 解:根据题意可得①$\left\{\begin{array}{l}{2x-3>0}\\{1+3x<0}\end{array}\right.$或②$\left\{\begin{array}{l}{2x-3<0}\\{1+3x>0}\end{array}\right.$,
解不等式组①,知该不等式组无解;
解不等式组②,得-$\frac{1}{3}$<x<$\frac{3}{2}$,
∴该不等式的解集为-$\frac{1}{3}$<x<$\frac{3}{2}$.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
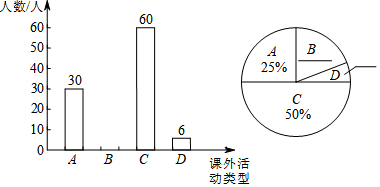
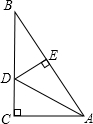 在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于11.4cm.
在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于11.4cm. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
 如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO.
如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO. 已知:如图,在△ABC中,D、E、F是分别是三边BC、AC、AB的中点,连接EF、AD.
已知:如图,在△ABC中,D、E、F是分别是三边BC、AC、AB的中点,连接EF、AD.