题目内容
16.若a,b,c三个数满足a2+b2+c2=ab+bc+ac,则( )| A. | a=b=c | B. | a,b,c不全相等 | ||
| C. | a,b,c互不相等 | D. | 无法确定a,b,c之间关系 |
分析 将原式两边都乘以2,移项后运用完全平方公式配成完全平方式结合非负数性质可得.
解答 解:原式可化为2a2+2b2+2c2=2ab+2ac+2bc,
即a2+b2+c2+a2+b2+c2-2ab-2ac-2bc=0;
根据完全平方公式,得:(a-b)2+(c-a)2+(b-c)2=0;
由非负数的性质,可知:a-b=0,c-a=0,b-c=0;
即:a=b=c;
故选:A.
点评 本题主要考查因式分解的应用能力,灵活运用完全平方公式,将原式两边乘以2以配成完全平方式是关键.

练习册系列答案
相关题目
3.若x+x-1=a,则$\frac{{x}^{4}+1}{{x}^{2}}$等于(用含a的代数式表示)( )
| A. | a2+2 | B. | a2-2 | C. | a4+4 | D. | a4-4 |
4.下列各组数中,属于勾股数的是( )
| A. | 2.5,6,6.5 | B. | 5,7,10 | C. | $\sqrt{2},\sqrt{3},\sqrt{5}$ | D. | 6,8,10 |
11.某市的中考各科试卷总分为600分,其中数学为120分,若用扇形统计图画出各科分数比例,则数学所占扇形圆心角为( )度.
| A. | 90 | B. | 45 | C. | 120 | D. | 72 |
1.下列各组中的两个“F”,通过平移可以重合在一起的是( )
| A. |  | B. |  | C. |  | D. |  |
5.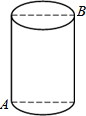 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
6.国务院总理作2009年政府工作报告时表示,今后三年各级政府拟投入医疗卫生领域的资金将达到850000000000元人民币,将数字850000000000用科学记数法表示为( )
| A. | 8.5×109 | B. | 8.5×1010 | C. | 8.5×1011 | D. | 8.5×1012 |
 如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).当t=$\frac{280}{183}$秒时,∠EPF=90°.
如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).当t=$\frac{280}{183}$秒时,∠EPF=90°.