题目内容
20.若等式$\sqrt{(x-2)(x+1)}$=$\sqrt{x-2}$$•\sqrt{x+1}$成立,则x的取值范围是( )| A. | x≥2 | B. | x≥1 | C. | -1≤x≤2 | D. | x≤-1或x≥2 |
分析 根据二次根式的乘法:$\sqrt{ab}=\sqrt{a}•\sqrt{b}$(a≥0,b≥0),即可解答.
解答 解:∵等式$\sqrt{(x-2)(x+1)}$=$\sqrt{x-2}$$•\sqrt{x+1}$成立,
∴$\left\{\begin{array}{l}{x-2≥0}\\{x+1≥0}\end{array}\right.$
解得:x≥2,
故选:A.
点评 本题考查了二次根式的乘法,解决本题的关键是熟记二次根式的乘法:$\sqrt{ab}=\sqrt{a}•\sqrt{b}$(a≥0,b≥0).

练习册系列答案
相关题目
7.下列个数中,不是无理数的是( )
| A. | 0.$\stackrel{.}{5}$ | B. | $\sqrt{7}$ | C. | π | D. | 0.151151115… |
11.某市的中考各科试卷总分为600分,其中数学为120分,若用扇形统计图画出各科分数比例,则数学所占扇形圆心角为( )度.
| A. | 90 | B. | 45 | C. | 120 | D. | 72 |
5.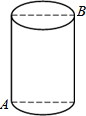 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
12.为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费.如图是张磊家2015年9月和10月所交电费的收据,则该市规定的第一阶梯电价和第二阶梯电价分别为每度( )
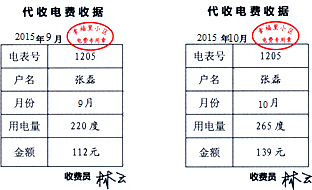

| A. | 0.5元、0.6元 | B. | 0.4元、0.5元 | C. | 0.3元、0.4元 | D. | 0.6元、0.7元 |
9.已知一次函数y=2x+2与x轴y轴分别交于A、B两点,另一直线y=kx+3交x轴正半轴于E、交y轴于F点,如△AOB与E、F、O三点组成的三角形相似,那么k值为( )
| A. | -0.5 | B. | -2 | C. | -0.5或-2 | D. | 以上都不对 |
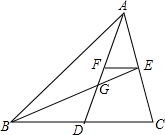 如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.