题目内容
6.计算:($\frac{{b}^{2}}{{a}^{2}}$-$\frac{{a}^{2}}{{b}^{2}}$)($\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$-1)($\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$+1).分析 先算括号里面的,再算乘法即可.
解答 解:原式=$\frac{{b}^{4}-{a}^{4}}{{a}^{2}{b}^{2}}$•[$\frac{{b}^{4}+{a}^{4}}{{a}^{2}{b}^{2}}$-1]•[$\frac{{b}^{4}+{a}^{4}}{{a}^{2}{b}^{2}}$+1]
=$\frac{{b}^{4}-{a}^{4}}{{a}^{2}{b}^{2}}$•[($\frac{{b}^{4}+{a}^{4}}{{a}^{2}{b}^{2}}$)2-1]
=$\frac{{b}^{4}-{a}^{4}}{{a}^{2}{b}^{2}}$•$\frac{{(a}^{4}+{b}^{4})^{2}}{{a}^{4}{b}^{4}}$-$\frac{{b}^{4}-{a}^{4}}{{a}^{2}{b}^{2}}$
=$\frac{{{(a}^{4}+{b}^{4})}^{2}{(b}^{4}-{a}^{4})}{{a}^{6}{b}^{6}}$-$\frac{({b}^{4}-{a}^{4})•{a}^{4}{b}^{4}}{{a}^{6}{b}^{6}}$
=$\frac{{{(a}^{4}+{b}^{4})}^{\;}{(b}^{8}-{a}^{8})}{{a}^{6}{b}^{6}}$-$\frac{({b}^{4}-{a}^{4})•{a}^{4}{b}^{4}}{{a}^{6}{b}^{6}}$
=$\frac{{a}^{4}{b}^{8}-{a}^{12}+{b}^{12}-{a}^{8}{b}^{4}-{a}^{4}{b}^{8}+{a}^{8}{b}^{4}}{{a}^{6}{b}^{6}}$
=$\frac{{b}^{12}-{a}^{12}}{{a}^{6}{b}^{6}}$.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

| A. | 0个 | B. | 1个 | ||
| C. | 无数个 | D. | 0个或1个或无数个 |
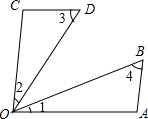 如图,∠1=∠2,CD∥OA,AB∥OC,求证:∠3=∠4.
如图,∠1=∠2,CD∥OA,AB∥OC,求证:∠3=∠4. 已知点A(-1,2),点C(2,1)沿0A方向平移$\sqrt{5}$个单位得出点B,判断四边形0ABC的形状,并证明你的结论;求出直线0A和BC之间的距离.
已知点A(-1,2),点C(2,1)沿0A方向平移$\sqrt{5}$个单位得出点B,判断四边形0ABC的形状,并证明你的结论;求出直线0A和BC之间的距离.