题目内容
15.设m、n为整数,则两个奇数可分别表示为2m+1和2n+1.试运用因式分解的知识证明两个奇数的平方差即(2m+1)2-(2n+1)2是8的倍数.分析 利用平方差公式因式分解,进一步计算提取公因式后证得结论即可.
解答 证明:(2m+1)2-(2n+1)2=(2m+1-2n-1)(2m+1+2n+1)=4(m-n)(m+n+1),
∵m、n为整数,
∴m-n或m+n+1必有一个是偶数,
∴4(m-n)(m+n+1)一定能被8整除,
∴(2m+1)2-(2n+1)2是8的倍数.
点评 此题考查因式分解的实际运用,掌握平方差公式是解决问题的前提,注意数的奇偶性的运用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
5.如果函数y=3x-2与y=2x+b的图象相交于y轴,那么b的值是( )
| A. | -2 | B. | -$\frac{2}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
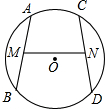 如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD=6.
如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD=6.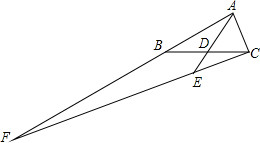 如图,D为BC边的中点,EC=$\frac{1}{4}$CF,求$\frac{AF}{AB}$的值.
如图,D为BC边的中点,EC=$\frac{1}{4}$CF,求$\frac{AF}{AB}$的值.