题目内容
18.已知抛物线顶点坐标为A,直线l与x轴平行,且与抛物线交于B(1,1),C(5,1)两点,若S△ABC=6,求该抛物线解析式.分析 由于B点和C点为抛物线上的对称点,则可设A(3,t),利用三角形面积公式得到$\frac{1}{2}$•(5-1)•|t-1|=6,解得t1=4,t2=-2,则A(3,4)或(3,-2),然后分别设顶点式求抛物线解析式.
解答 解:设A(3,t),
∵S△ABC=6,
∴$\frac{1}{2}$•(5-1)•|t-1|=6,解得t1=4,t2=-2,
当A(3,4)时,设抛物线解析式为y=a(x-3)2+4,把B(1,1)代入得a•(1-3)2+4=1,解得a=-$\frac{3}{4}$,此时抛物线解析式为y=-$\frac{3}{4}$(1-3)2+4;
当A(3,-2)时,设抛物线解析式为y=a(x-3)2-2,把B(1,1)代入得a•(1-3)2-2=1,解得a=$\frac{3}{4}$,此时抛物线解析式为y=$\frac{3}{4}$(1-3)2-2.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8.在Rt△ACB中,∠C=90°,AB=10,sinA=$\frac{3}{5}$,则BC的长为( )
| A. | 6 | B. | 7.5 | C. | 8 | D. | 12.5 |
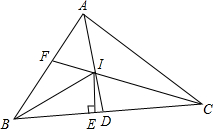 如图所示,I是△ABC三内角平分线的交点,IE⊥BC于E,AI延长线交BC于D,CI的延长线交AB于F,下列结论:①∠BIE=∠CID;②S△ABC=$\frac{1}{2}$IE(AB+BC+AC);③BE=$\frac{1}{2}$(AB+BC-AC);④AC=AF+DC.其中正确的结论是( )
如图所示,I是△ABC三内角平分线的交点,IE⊥BC于E,AI延长线交BC于D,CI的延长线交AB于F,下列结论:①∠BIE=∠CID;②S△ABC=$\frac{1}{2}$IE(AB+BC+AC);③BE=$\frac{1}{2}$(AB+BC-AC);④AC=AF+DC.其中正确的结论是( ) 如图,在△ABC中,∠B=30°,AB=BC=6cm,AC=4cm.
如图,在△ABC中,∠B=30°,AB=BC=6cm,AC=4cm.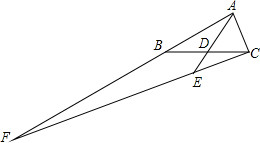 如图,D为BC边的中点,EC=$\frac{1}{4}$CF,求$\frac{AF}{AB}$的值.
如图,D为BC边的中点,EC=$\frac{1}{4}$CF,求$\frac{AF}{AB}$的值.