题目内容
16.1m长的绳子,第一次截去一半,第2次截去剩下的一半,如此截下去,第5次后剩下的绳子的长为$\frac{1}{32}$m;第n次后剩下的绳子的长为($\frac{1}{2}$)nm.分析 根据题意可得第一次截去一半可得$\frac{1}{2}$,第2次截去剩下的一半可得$\frac{1}{4}$,第3次截去剩下的一半$\frac{1}{8}$,依次截下去可得第n次后剩下的绳子的长为($\frac{1}{2}$)nm.
解答 解:由题意得:($\frac{1}{2}$)5×1=$\frac{1}{32}$,
第n次后剩下的绳子的长为::($\frac{1}{2}$)n×1=($\frac{1}{2}$)n.
故答案为:$\frac{1}{32}$;($\frac{1}{2}$)n.
点评 此题主要考查了列代数式,关键是正确理解题意,找出题目中的数量关系.

练习册系列答案
相关题目
5.如果函数y=3x-2与y=2x+b的图象相交于y轴,那么b的值是( )
| A. | -2 | B. | -$\frac{2}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
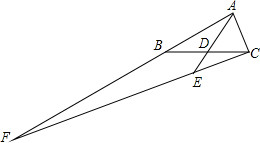 如图,D为BC边的中点,EC=$\frac{1}{4}$CF,求$\frac{AF}{AB}$的值.
如图,D为BC边的中点,EC=$\frac{1}{4}$CF,求$\frac{AF}{AB}$的值.