题目内容
6.已知x1,x2是一元二次方程x2-2x-1=0的两根,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-2.分析 利用韦达定理求得x1+x2=2,x1•x2=-1,然后将其代入通分后的所求代数式并求值.
解答 解:∵一元二次方程x2-2x-1=0的两根为x1、x2,
x1+x2=2,
x1•x2=-1,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-2.
故答案是:-2.
点评 此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
17.九年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多”乙说:“二班同学投中次数最多与最少的相差6个.”上面两名同学的议论能反映出的统计量是( )
| A. | 平均数和众数 | B. | 众数和极差 | C. | 众数和方差 | D. | 中位数和极差 |
14.在-1,-2,0,1这4个数中最小的一个是( )
| A. | -1 | B. | 0 | C. | -2 | D. | 1 |
1.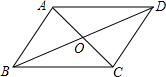 如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
 如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )| A. | AB=AD | B. | AC⊥BD | C. | AC=BD | D. | ∠BAC=∠DAC |
 如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)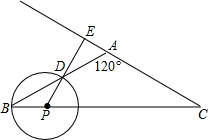 如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E.
如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E.
 如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.