题目内容
3. 如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.
分析 连接AD,先根据线段垂直平分线的性质得出AD=BD,再设BD=x,则AD=8-x,再根据勾股定理求出x的值即可.
解答  解:连接AD,
解:连接AD,
∵AB的垂直平分线交AB于E,
∴AD=BD,
设BD=x,则AD=8-x,
在Rt△ACD中,
∵AC=3,CD=8-x,AD=x,
∴AC2+CD2=AD2,
即32+(8-x)2=x2,
解得x=$\frac{25}{8}$,
即BD=$\frac{25}{8}$.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
7.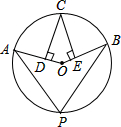 如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
 如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )| A. | 140° | B. | 70° | C. | 60° | D. | 40° |
4.下表是某校女子排球队队员的年龄分布
则该校女子排球队队员的平均年龄是15岁.
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 频数 | 1 | 1 | 7 | 3 |
15.下列方程的变形中,正确的是( )
| A. | 由$-\frac{1}{3}$x=0,得x=3 | B. | 由6y=3,得y=2 | ||
| C. | 由x-5=-3,得x=5+3 | D. | 由2=x-4,得x=4+2 |
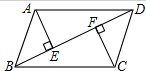 如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.