题目内容
17．九年级一班和二班每班选8名同学进行投篮比赛，每名同学投篮10次，对每名同学投中的次数进行统计，甲说：“一班同学投中次数为6个的最多”乙说：“二班同学投中次数最多与最少的相差6个．”上面两名同学的议论能反映出的统计量是（ ）| A． | 平均数和众数 | B． | 众数和极差 | C． | 众数和方差 | D． | 中位数和极差 |
分析 根据众数和极差的概念进行判断即可．
解答 解：一班同学投中次数为6个的最多反映出的统计量是众数，
二班同学投中次数最多与最少的相差6个能反映出的统计量极差，
故选：B．
点评 本题考查的是统计量的选择，平均数、众数、中位数和极差、方差在描述数据时的区别：①数据的平均数、众数、中位数是描述一组数据集中趋势的特征量，极差、方差是衡量一组数据偏离其平均数的大小（即波动大小）的特征数，描述了数据的离散程度．②极差和方差的不同点：极差表示一组数据波动范围的大小，一组数据极差越大，则它的波动范围越大．
练习册系列答案
阅读快车系列答案
相关题目
7．数学老师将全班分成7个小组开展小组合作学习，采用随机抽签确定一个小组进行展示活动，则第3个小组被抽到的概率是（ ）
| A． | $\frac{1}{7}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{21}$ | D． | $\frac{1}{10}$ |
8．2016年5月下旬，中国大数据博览会在贵阳举行，参加此次大会的人数约有89000人，将89000用科学记数法表示为（ ）
| A． | 89×103 | B． | 8.9×104 | C． | 8.9×103 | D． | 0.89×105 |
5．
如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（ ）
如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（ ）| A． | 2 | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的表面积为4πcm2．
如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其部分图象如图所示，下列结论：
如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，连接MC，将菱形ABCD翻折，使点A落在线段CM上的点E处，折痕交AB于点N，则线段EC的长为$\sqrt{7}$-1．
7．
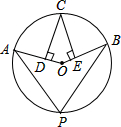如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，则∠P的度数为（ ）
如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，则∠P的度数为（ ）| A． | 140° | B． | 70° | C． | 60° | D． | 40° |