题目内容
16.(2+1)(22+1)(24+1)(28+1)(216+1)的计算结果的个位数字是( )| A. | 8 | B. | 5 | C. | 4 | D. | 2 |
分析 原式变形后,利用平方差公式计算得到结果,归纳总结即可确定出结果的个位数字.
解答 解:原式=(2-1)•(2+1)•(22+1)•(24+1)…(216+1)
=(22-1)•(22+1)•(24+1)…(216+1)
=(24-1)•(24+1)…(216+1)
=232-1
=232-1
∵21=2,22=4,23=8,24=16,25=32,…,
∴其结果个位数以2,4,8,6循环,
∵32÷4=8,
∴232的个位数字为6,
∴原式的个位数字为6-1=5.
故选:B.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
7.分式$\frac{1}{x-1}$有意义,则x的值为( )
| A. | x=1 | B. | x≠0 | C. | x≠1 | D. | x=0 |
11.甲打360个字与乙打480个字所用时间相同,已知两人每分钟共打140个字.若设甲每分钟打x个字,则可列方程( )
| A. | $\frac{360}{x}$=$\frac{480}{140-x}$ | B. | $\frac{480}{x}$=$\frac{360}{140-x}$ | C. | $\frac{360}{x}$+$\frac{480}{x}$=140 | D. | x+$\frac{360x}{480}$=140 |
5. 如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
 如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )| A. | $\sqrt{74}$ | B. | $\sqrt{74}$+3 | C. | $\sqrt{74}$-3 | D. | 3 |
17.在同一平面内,∠AOB=70°,∠BOC=40°,则∠AOC的度数为( )
| A. | 110° | B. | 30° | C. | 110°或150° | D. | 30°或110° |
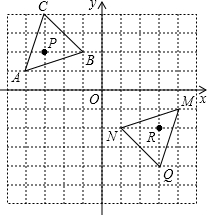 如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.
如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.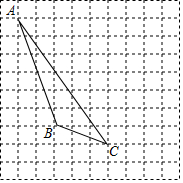 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.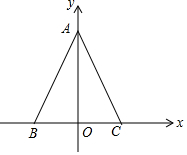 如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0).
如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0).