题目内容
1.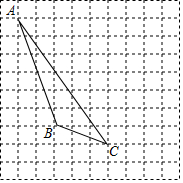 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)画出△ABC中AB边上的中线CM;
(3)画出△ABC中AB边上的高CD,垂足是D;
(4)图中△ABC的面积是8.
分析 (1)根据图形平移的性质画出△A1B1C1即可;
(2)根据格点的特点作出AB边上的中线CM即可;
(3)过点C向AB边的延长线作垂线,垂足为点D即可;
(4)利用矩形的面积减去三个顶点上三角形的面积和两个格点的面积即可.
解答  解:(1)如图,△A1B1C1即为所求;
解:(1)如图,△A1B1C1即为所求;
(2)如图,CM即为所求;
(3)如图,CD即为所求;
(4)S△ABC=7×5-2-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×6-$\frac{1}{2}$×5×7
=35-2-$\frac{3}{2}$-6-$\frac{35}{2}$
=8.
故答案为:8.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
11.下列性质中,平行四边形不一定具备的是( )
| A. | 邻角互补 | B. | 对角互补 | C. | 对边相等 | D. | 对角线互相平分 |
9.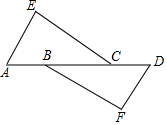 如图,AE∥FD,AB=CD,要使△EAC≌△FDB,需要添加下列选项中的( )
如图,AE∥FD,AB=CD,要使△EAC≌△FDB,需要添加下列选项中的( )
 如图,AE∥FD,AB=CD,要使△EAC≌△FDB,需要添加下列选项中的( )
如图,AE∥FD,AB=CD,要使△EAC≌△FDB,需要添加下列选项中的( )| A. | ∠A=∠D | B. | AE=DF | C. | EC=BF | D. | BC=CD |
16.(2+1)(22+1)(24+1)(28+1)(216+1)的计算结果的个位数字是( )
| A. | 8 | B. | 5 | C. | 4 | D. | 2 |
10.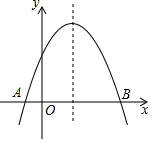 函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )
函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )
 函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )
函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )| A. | $\frac{1}{3}$或2 | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
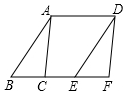 如图,面积为8cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中四边形ACED的面积是24cm2.
如图,面积为8cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中四边形ACED的面积是24cm2.