题目内容
15.计算(1)8+(-10)+(-2)-(-5)
(2)$2\frac{1}{3}-\frac{2}{5}-\frac{3}{5}+(-1\frac{1}{3})$
(3)$(-\frac{3}{4})×\frac{3}{8}÷(-\frac{9}{16})$
(4)1÷(-2)+0÷4-(-4)×(-1)
(5)$(\frac{5}{6}-\frac{7}{9}+1\frac{3}{4})×(-36)$
(6)19$\frac{23}{24}$×(-12)
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式结合后,相加即可得到结果;
(3)原式从左到右依次计算即可得到结果;
(4)原式先计算乘除运算,再计算加减运算即可得到结果;
(5)原式利用乘法分配律计算即可得到结果;
(6)原式变形后,利用乘法分配律计算即可得到结果.
解答 解:(1)原式=8-10-2+5=13-12=1;
(2)原式=2$\frac{1}{3}$-1$\frac{1}{3}$-$\frac{2}{5}$-$\frac{3}{5}$=1-1=0;
(3)原式=$\frac{3}{4}$×$\frac{3}{8}$×$\frac{16}{9}$=$\frac{1}{2}$;
(4)原式=-$\frac{1}{2}$+0-4=-4$\frac{1}{2}$;
(5)原式=-30+28-63=-65;
(6)原式=(20-$\frac{1}{24}$)×(-12)=-240+$\frac{1}{2}$=-239$\frac{1}{2}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
6.若多项式3x2y2-2xy-x+8y与某多项式的差为x2-2x+1,则这个多项式为( )
| A. | 3x2y2-2xy-x2+8y-3x-1 | B. | 3x2y2-2xy-x2+8y-3x+1 | ||
| C. | 3x2y2-2xy-x2+8y+x+1 | D. | 3x2y2-2xy-x2+8y+x-1 |
20.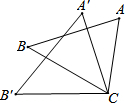 如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
 如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |




 如图,在△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:△ABD≌△AEC.
如图,在△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:△ABD≌△AEC.