题目内容
将多项式m4+2m2-3分解因式结果是 ．
考点：因式分解-十字相乘法等
专题：
分析：首先利用十字相乘法分解因式，进而利用平方差公式分解因式得出即可．
解答：解：m4+2m2-3
=（m2+3）（m2-1）
=（m2+3）（m-1）（m+1）．
故答案为：（m2+3）（m-1）（m+1）．
=（m2+3）（m2-1）
=（m2+3）（m-1）（m+1）．
故答案为：（m2+3）（m-1）（m+1）．
点评：此题主要考查了十字相乘法、平方差公式分解因式，熟练利用十字相乘法分解因式是解题关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
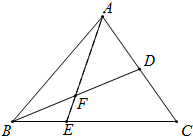如图，在△ABC中E是BC上的一点，EC=2EB，点D是AC的中点，AE、BD交于点F，AF=3FE．若△ABC的面积为18，给出下列命题：计算的（-a）3•（-a）4结果是（ ）
| A、a7 |
| B、-a12 |
| C、a12 |
| D、-a7 |