题目内容
在矩形ABCD中,AB=2,AD=2
,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是点E、F,点Q关于直线BC、CD的对称点分别是G、H.若由E、F、G、H构成的四边形恰好为菱形,则该菱形的边长为 .
| 2 |
考点:菱形的判定,矩形的性质,轴对称的性质
专题:
分析:首先根据题意画出图形,可证明矩形的四个顶点A、B、C、D均在菱形EFGH的边上,且点A、C分别为各自边的中点;继而证明菱形的边长等于矩形的对角线长;然后求出线段AP的长度,证明△AOP为等腰三角形;再利用勾股定理求出线段OP的长度;则同理求出OQ的长度,从而得到PQ的长度.
解答: 解:由矩形ABCD中,AB=2,AD=2
解:由矩形ABCD中,AB=2,AD=2
,可得对角线AC=BD=
=2
.
依题意画出图形,如右图所示.
由轴对称性质可知,∠PAF+∠PAE=2∠PAB+2∠PAD=2(∠PAB+∠PAD)=180°,
∴点A在菱形EFGH的边EF上.
同理可知,点B、C、D均在菱形EFGH的边上.
∵AP=AE=AF,
∴点A为EF中点.
同理可知,点C为GH中点.
连接AC,交BD于点O,则有AF=CG,且AF∥CG,
∴四边形ACGF为平行四边形,
∴FG=AC=2
,
即菱形EFGH的边长等于矩形ABCD的对角线长.
∴EF=FG=2
,
∵AP=AE=AF,
∴AP=
EF=
.
∵OA=
AC=
,
∴AP=AO,
即△APO为等腰三角形.
过点A作AN⊥BD交BD于点N,则点N为OP的中点.
由S△ABD=
AB•AD=
AC•AN,
可求得:AN=
.
在Rt△AON中,由勾股定理得:ON=
=
,
∴OP=2ON=
;
同理可求得:OQ=
,
∴PQ=OP+OQ=
.
故答案为:
.
 解:由矩形ABCD中,AB=2,AD=2
解:由矩形ABCD中,AB=2,AD=2| 2 |
| AB2+CD2 |
| 3 |
依题意画出图形,如右图所示.
由轴对称性质可知,∠PAF+∠PAE=2∠PAB+2∠PAD=2(∠PAB+∠PAD)=180°,
∴点A在菱形EFGH的边EF上.
同理可知,点B、C、D均在菱形EFGH的边上.
∵AP=AE=AF,
∴点A为EF中点.
同理可知,点C为GH中点.
连接AC,交BD于点O,则有AF=CG,且AF∥CG,
∴四边形ACGF为平行四边形,
∴FG=AC=2
| 3 |
即菱形EFGH的边长等于矩形ABCD的对角线长.
∴EF=FG=2
| 3 |
∵AP=AE=AF,
∴AP=
| 1 |
| 2 |
| 3 |
∵OA=
| 1 |
| 2 |
| 3 |
∴AP=AO,
即△APO为等腰三角形.
过点A作AN⊥BD交BD于点N,则点N为OP的中点.
由S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
可求得:AN=
2
| ||
| 3 |
在Rt△AON中,由勾股定理得:ON=
| OA2-AN2 |
| ||
| 3 |
∴OP=2ON=
2
| ||
| 3 |
同理可求得:OQ=
2
| ||
| 3 |
∴PQ=OP+OQ=
4
| ||
| 3 |
故答案为:
4
| ||
| 3 |
点评:本题是几何变换综合题,难度较大.首先根据题意画出图形,然后结合轴对称性质、矩形性质、菱形性质进行分析,明确线段之间的数量关系,最后由等腰三角形和勾股定理求得结果.

练习册系列答案
相关题目
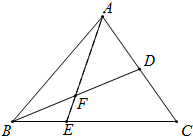 如图,在△ABC中E是BC上的一点,EC=2EB,点D是AC的中点,AE、BD交于点F,AF=3FE.若△ABC的面积为18,给出下列命题:
如图,在△ABC中E是BC上的一点,EC=2EB,点D是AC的中点,AE、BD交于点F,AF=3FE.若△ABC的面积为18,给出下列命题: