题目内容
如图,正方形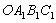 的边长为2,以
的边长为2,以 为圆心、
为圆心、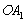 为半径作弧
为半径作弧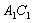 交
交 于点
于点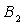 ,设弧
,设弧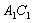 与边
与边 、
、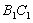 围成的阴影部分面积为
围成的阴影部分面积为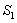 ;然后以
;然后以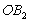 为对角线作正方形
为对角线作正方形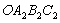 ,又以
,又以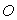 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交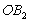 于点
于点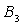 ,设弧
,设弧 与边
与边 、
、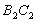 围成的阴影部分面积为
围成的阴影部分面积为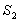 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边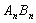 、
、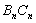 围成的阴影部分面积为
围成的阴影部分面积为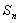 .则:(1)
.则:(1)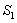 = ;(2)
= ;(2)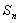 = .
= .

(1) 4-π.(2)  .
.
【解析】第一个阴影部分的面积都等于它所在正方形的面积-扇形的面积.依此公式计算.S1=4- =4-π.
=4-π.
根据勾股定理得:OB1=
则OB2=2,
∴B1B2=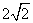 -2,
-2,
再根据勾股定理得:2OA22=(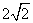 -2)2解得:OA22=6-
-2)2解得:OA22=6- .
.
则阴影的面积=6- -
- =6-
=6- -
- .
.
从而我们可以发现规律,并用Sn= 表示.
表示.

练习册系列答案
相关题目
 中自变量
中自变量 的取值范围是 .
的取值范围是 . 于H,折痕为EF,联结BP、BH.
于H,折痕为EF,联结BP、BH.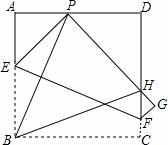

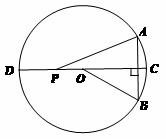
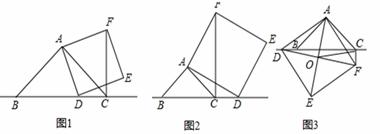
 ,对角线AE,DF相交于点O,连接OC 求OC的长度.
,对角线AE,DF相交于点O,连接OC 求OC的长度. 6w=100.求x+y+z+w的最大值和最小值
6w=100.求x+y+z+w的最大值和最小值
 例如:[5.7]=5,[5]=5,[-π]=-4.
例如:[5.7]=5,[5]=5,[-π]=-4.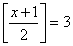
 ,满足条件的所有正整数
,满足条件的所有正整数 x有___________
x有___________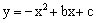 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与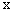 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。