题目内容
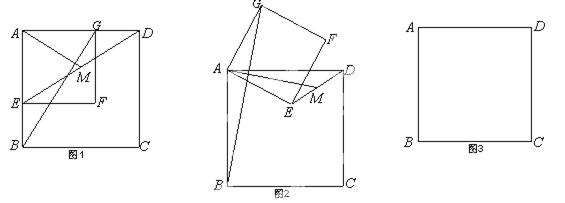
如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC 于H,折痕为EF,联结BP、BH.
于H,折痕为EF,联结BP、BH.
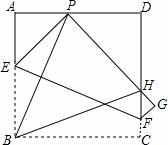
(1)求证:∠APB=∠BPH;
(2)求证:AP+ HC=PH;
HC=PH;
(3)当AP=1时,求PH的长.
(1)证明见解析;(2)证明见解析;(3)3.4.
【解析】(1)∵PE=BE,∴∠EPB=∠EBP,又∵∠EPH=∠EBC=90°,∴∠EPH-∠EPB=∠EBC-∠EBP.即∠BPH=∠PBC.又∵四边形ABCD为正方形∴AD∥BC,∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)过B作BQ⊥PH,垂足为Q,

由(1)知,∠APB=∠BPH,在△ABP与△QBP中, ,∴△ABP≌△QBP(AAS),∴AP=QP,BA=BQ.又∵AB=BC,∴BC=BQ.又∵∠C=∠BQH=90°,∴△BCH和△BQH是直角三角形,在Rt△BCH与Rt△BQH中,
,∴△ABP≌△QBP(AAS),∴AP=QP,BA=BQ.又∵AB=BC,∴BC=BQ.又∵∠C=∠BQH=90°,∴△BCH和△BQH是直角三角形,在Rt△BCH与Rt△BQH中, ,∴Rt△BCH≌Rt△BQH(HL),∴CH=QH,∴AP+HC=PH.
,∴Rt△BCH≌Rt△BQH(HL),∴CH=QH,∴AP+HC=PH.
(3)由(2)知,AP=PQ=1,∴PD=3.设QH=HC=x,则DH=4-x.在Rt△PDH中,PD2+DH2=PH2,
即32+(4-x)2=(x+1)2,解得x=2.4,∴PH=3.4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 则tan∠MCN=
则tan∠MCN= 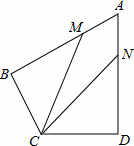
 角(
角(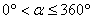 )得到
)得到 ,点P的对应点为
,点P的对应点为
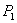 ,连
,连 ,在旋转过程中,线段
,在旋转过程中,线段
 ),y随x变化的图象可能是( )
),y随x变化的图象可能是( )

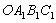 的边长为2,以
的边长为2,以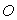 为圆心、
为圆心、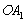 为半径作弧
为半径作弧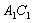 交
交 于点
于点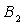 ,设弧
,设弧 、
、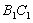 围成的阴影部分面积为
围成的阴影部分面积为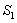 ;然后以
;然后以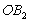 为对角线作正方形
为对角线作正方形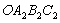 ,又以
,又以 为半径作弧
为半径作弧 交
交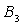 ,设弧
,设弧 、
、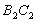 围成的阴影部分面积为
围成的阴影部分面积为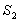 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边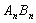 、
、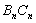 围成的阴影部分面积为
围成的阴影部分面积为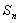 .则:(1)
.则:(1)
 为
为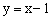 ,直接
,直接 向所成的角为600,①求直线l4的函数表达式;②把直线l4绕点(1,0)按逆时针方向旋转900得到的直线l5,求直线l5的函数表达式;
向所成的角为600,①求直线l4的函数表达式;②把直线l4绕点(1,0)按逆时针方向旋转900得到的直线l5,求直线l5的函数表达式; 有何关系?请根据猜想结论直接写出过点(1,0)且与直线
有何关系?请根据猜想结论直接写出过点(1,0)且与直线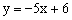 垂直的直线l6的函数表达式。
垂直的直线l6的函数表达式。