题目内容
如图,抛物线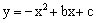 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与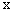 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。
(1)求抛物线的解析式;
(2)连接AC,CD,AD,试证明△ACD为直角三角形;
(3)若点E在抛物线上,EF⊥x轴于点F,以A、E、F为顶点的三角形与△ACD相似,试求出所有满足条件的点E的坐标。

(1)由题意得  ,解得:
,解得: ,
,
∴解析式的 解析式为:
解析式为: 。
。

(3)设E ,分两种情况讨论:
,分两种情况讨论:

①若△A FE∽△ACD,如图1,则
FE∽△ACD,如图1,则 ,即
,即 ,
,
整理,得 ,解得
,解得 (与点A重合,舍去),
(与点A重合,舍去),
当 时,
时, 。
。
∴此时,点E 的坐标为
的坐标为 。
。


【考点】二次函数综合题,二次函数顶点,直角三角形的判定,勾股定理和逆定理,相似三角形的性质,解一元二次方程,分类思想的应用。


练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
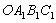 的边长为2,以
的边长为2,以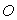 为圆心、
为圆心、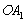 为半径作弧
为半径作弧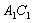 交
交 于点
于点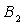 ,设弧
,设弧 、
、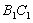 围成的阴影部分面积为
围成的阴影部分面积为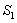 ;然后以
;然后以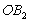 为对角线作正方形
为对角线作正方形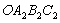 ,又以
,又以 为半径作弧
为半径作弧 交
交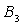 ,设弧
,设弧 、
、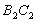 围成的阴影部分面积为
围成的阴影部分面积为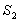 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边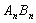 、
、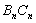 围成的阴影部分面积为
围成的阴影部分面积为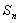 .则:(1)
.则:(1)
 为
为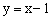 ,直接
,直接 向所成的角为600,①求直线l4的函数表达式;②把直线l4绕点(1,0)按逆时针方向旋转900得到的直线l5,求直线l5的函数表达式;
向所成的角为600,①求直线l4的函数表达式;②把直线l4绕点(1,0)按逆时针方向旋转900得到的直线l5,求直线l5的函数表达式; 有何关系?请根据猜想结论直接写出过点(1,0)且与直线
有何关系?请根据猜想结论直接写出过点(1,0)且与直线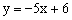 垂直的直线l6的函数表达式。
垂直的直线l6的函数表达式。
 的图象如下列四个图之一所示,根据
的图象如下列四个图之一所示,根据 图象分析,a的值等于【 】
图象分析,a的值等于【 】
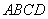
 ,花园的一边靠墙,另三边用总长为40m的栅栏围
,花园的一边靠墙,另三边用总长为40m的栅栏围 成(如图所示).若设花园的
成(如图所示).若设花园的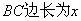
 (m),花园的面积为
(m),花园的面积为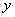

 (m
(m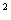
 ).
).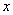
 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量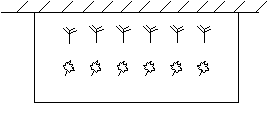

 x+b(a>0)、二次函数y=ax2+bx和反比例函数y=
x+b(a>0)、二次函数y=ax2+bx和反比例函数y=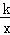
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )

 方程
方程 有实数根x1,x2,且x1≠x2,有下列结论:
有实数根x1,x2,且x1≠x2,有下列结论: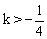 ;
; 的图象与x轴交点的坐标
的图象与x轴交点的坐标 (1,0)和(2,0)。
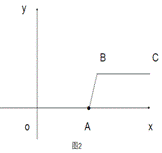
(1,0)和(2,0)。 长方形ACBD和长方形AEFB(如图2)。
长方形ACBD和长方形AEFB(如图2)。

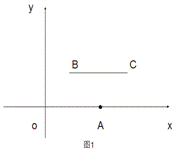
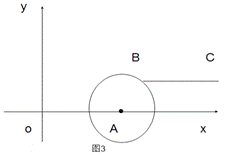
 中的要求把它补成长方形,那么符合要求的长方形可以画出 个,利用图3把它画出来。
中的要求把它补成长方形,那么符合要求的长方形可以画出 个,利用图3把它画出来。 =2时,如图1,线段BC与线段OA的距离是_____,
=2时,如图1,线段BC与线段OA的距离是_____,