题目内容
6. 七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 12% |
| 5<x≤10 | 12 | 24% |
| 10<x≤15 | 16 | 32% |
| 15<x≤20 | 10 | 20% |
| 20<x≤25 | 4 | 8% |
| 25<x≤30 | 2 | 4% |
(Ⅰ)把上面的频数分布表和频数分布直方图补充完整;
(Ⅱ)观察上面的 频数分布表和频数分布直方图可知组距是5;
(Ⅲ)本次随机调查了多少户家庭?
(Ⅳ)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量不少于20t的家庭大约有多少户?
分析 (1)根据频数分布表提供的数据,运用公式:频率=频数÷数据总数,进行计算即可;
(2)观察频数分布直方图,可知组距的值;
(3)抽取的家庭数=频数÷频率,据此计算即可;
(4)根据月均用水量不少于20t的家庭数占抽取的家庭总数的百分比,乘上小区家庭总数,求得该小区月均用水量不少于20t的家庭数.
解答 解:(1)根据频数分布表可得,抽取的家庭数=6÷12%=50,
∴在5<x≤10一组,频数=50×24%=12,
在10<x≤15一组,频数=50×32%=16,
在20<x≤25一组,频率=4÷50=8%;
频数分布直方图如下:
(2)根据频数分布直方图可知,组距是5,
故答案为:5;
(3)由(1)可得,本次随机调查了50户家庭;
(4)该小区月均用水量不少于20t的家庭大约有(8%+4%)×1000=120(户).
点评 本题主要考查了频数分布表和频数分布直方图,解题时注意,在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.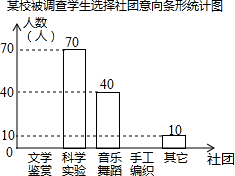 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
根据统计图表的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整(温馨提示:请画在答题卷相对应的图上);
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 文学鉴赏 | 科学检验 | 音乐舞蹈 | 手工编织 | 其他 |
| 所占百分比 | a | 20% | b | 10% | c |
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整(温馨提示:请画在答题卷相对应的图上);
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
11.若一个正数的平方根是2a-1和-a+2,则这个正数是( )
| A. | 1 | B. | 3 | C. | 4 | D. | 9 |
16.若a=(-$\frac{2}{3}$)-2,b=(-2016)0,c=(-0.2)-1,则a、b、c三数的大小关系是( )
| A. | a<b<c | B. | a>b>c | C. | a>c>b | D. | c>a>b |
 如图,在平面直角坐标系中,点A(0,8),点B(12,8),点C(18,0),连接AB,BC.
如图,在平面直角坐标系中,点A(0,8),点B(12,8),点C(18,0),连接AB,BC.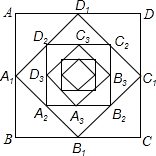 连结正方形四边中点所构成的正方形,我们称其原正方形的中点正方形,如图,已知正方形ABCD的中点正方形是A1B1C1D1,再作正方形A1B1C1D1的中点正方形A2B2C2D2,…这样不断地作下去,第n次所做的中点正方形 AnBnCnDn,若正方形ABCD的边长为1,则第10次所作的中点正方形边长为$\frac{1}{32}$,若设中点正方形 AnBnCnDn的面积为Sn,则S1+S2+S3+…+S10=$\frac{1023}{1024}$.
连结正方形四边中点所构成的正方形,我们称其原正方形的中点正方形,如图,已知正方形ABCD的中点正方形是A1B1C1D1,再作正方形A1B1C1D1的中点正方形A2B2C2D2,…这样不断地作下去,第n次所做的中点正方形 AnBnCnDn,若正方形ABCD的边长为1,则第10次所作的中点正方形边长为$\frac{1}{32}$,若设中点正方形 AnBnCnDn的面积为Sn,则S1+S2+S3+…+S10=$\frac{1023}{1024}$. 如图⊙O为△ABC的外接圆,∠A=70°,则∠BCO的度数为20°.
如图⊙O为△ABC的外接圆,∠A=70°,则∠BCO的度数为20°.