题目内容
小华的爸爸要用一块矩形铁皮加工出一个底面半径为20cm,高为40
cm的锥形漏斗,要求只能有一条接缝(接缝忽略不计)
(1)你能求出这个锥形漏斗的侧面展开图的圆心角吗?
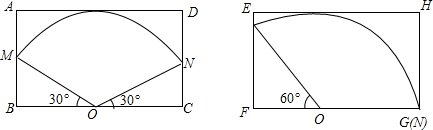
(2)如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?
| 2 |
(1)你能求出这个锥形漏斗的侧面展开图的圆心角吗?
(2)如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?

考点:圆锥的计算
专题:计算题
分析:(1)先根据勾股定理计算出母线长为60,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式计算锥形漏斗的侧面展开图的圆心角;
(2)如图1,矩形的一边长等于母线长60,再利用含30度的直角三角形三边的关系计算出OB,从而得到BC长,再计算矩形ABCD的面积;如图2,矩形的一边长等于母线长60,再利用含30度的直角三角形三边的关系计算出OF,从而得到CG长,再计算矩形EFGH的面积,然后比较两矩形的面积即可.
(2)如图1,矩形的一边长等于母线长60,再利用含30度的直角三角形三边的关系计算出OB,从而得到BC长,再计算矩形ABCD的面积;如图2,矩形的一边长等于母线长60,再利用含30度的直角三角形三边的关系计算出OF,从而得到CG长,再计算矩形EFGH的面积,然后比较两矩形的面积即可.
解答:解:(1)圆锥的母线长=
=60,
设这个锥形漏斗的侧面展开图的圆心角为n°,
所以2π•20=
,解得n=120,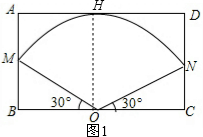
即这个锥形漏斗的侧面展开图的圆心角为120°;
(2)如图1,OM=60,∠MON=120°,
在Rt△OBM中,∵∠BOM=30°,
∴BM=30,
∴OB=
BM=30
,
∴BC=2OB=60
,
∴方案一所需的矩形铁皮的面积=60×60
=3600
,
如图2,OM=ON=60,∠MON=120°,
在Rt△FOM中,∵∠FOM=60°,
∴OF=30,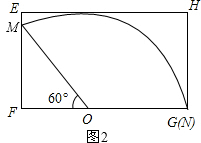
∴FG=OF+OG=30+60=90,
∴方案二所需的矩形铁皮的面积=90×60=5400,
∴方案二所用的矩形铁皮面积较少.
202+(40
|
设这个锥形漏斗的侧面展开图的圆心角为n°,
所以2π•20=
| n•π•60 |
| 180 |

即这个锥形漏斗的侧面展开图的圆心角为120°;
(2)如图1,OM=60,∠MON=120°,
在Rt△OBM中,∵∠BOM=30°,
∴BM=30,
∴OB=
| 3 |
| 3 |
∴BC=2OB=60
| 3 |
∴方案一所需的矩形铁皮的面积=60×60
| 3 |
| 3 |
如图2,OM=ON=60,∠MON=120°,
在Rt△FOM中,∵∠FOM=60°,
∴OF=30,

∴FG=OF+OG=30+60=90,
∴方案二所需的矩形铁皮的面积=90×60=5400,
∴方案二所用的矩形铁皮面积较少.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
抛物线y=x2-6x+5的对称轴为( )
| A、x=3 | ||
| B、x=-3 | ||
| C、x=6 | ||
D、x=-
|
 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )| A、30° | B、36° |
| C、50° | D、60° |
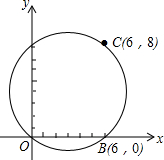 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.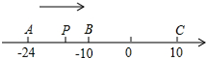 已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.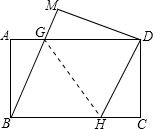 如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( )
如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( ) 如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.
如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.