题目内容
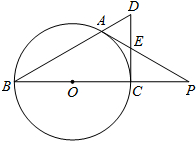 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D.若CD的中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D.若CD的中点E,AE的延长线与BC的延长线交于点P.(1)求证:AP是⊙O的切线;
(2)若OC=CP,CD=4,求⊙O半径的长.
考点:切线的判定
专题:
分析:(1)连接AO,AC(如图).欲证AP是⊙O的切线,只需证明OA⊥AP即可;
(2)由条件可求得∠P=30°,进一步可求得∠B=30°,在Rt△BCD中,由勾股定理可求得BC,进一步可求得半径.
(2)由条件可求得∠P=30°,进一步可求得∠B=30°,在Rt△BCD中,由勾股定理可求得BC,进一步可求得半径.
解答:(1)证明:连接AO,AC(如图).
∵BC是⊙O的直径,
∴∠BAC=∠CAD=90°.
∵E是CD的中点,
∴CE=DE=AE.
∴∠ECA=∠EAC.
∵OA=OC,
∴∠OAC=∠OCA.
∵CD是⊙O的切线,
∴CD⊥OC.
∴∠ECA+∠OCA=90°.
∴∠EAC+∠OAC=90°.
∴OA⊥AP.
∵A是⊙O上一点,
∴AP是⊙O的切线;
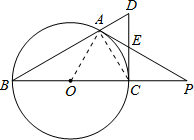
(2)解:由(1)知OA⊥AP,且OA=OC=CP,
∴∠P=30°,∠AOP=60°,
∴∠B=
∠AOP=30°,
在Rt△BCD中,CD=4,
∴BD=8,由勾股定理可求得BC=4
,
∴⊙O半径为2
.
∵BC是⊙O的直径,
∴∠BAC=∠CAD=90°.
∵E是CD的中点,
∴CE=DE=AE.
∴∠ECA=∠EAC.
∵OA=OC,
∴∠OAC=∠OCA.
∵CD是⊙O的切线,
∴CD⊥OC.
∴∠ECA+∠OCA=90°.
∴∠EAC+∠OAC=90°.
∴OA⊥AP.
∵A是⊙O上一点,
∴AP是⊙O的切线;

(2)解:由(1)知OA⊥AP,且OA=OC=CP,
∴∠P=30°,∠AOP=60°,
∴∠B=
| 1 |
| 2 |
在Rt△BCD中,CD=4,
∴BD=8,由勾股定理可求得BC=4
| 3 |
∴⊙O半径为2
| 3 |
点评:本题主要考查切线的性质和判定,已知切点连接圆心和切点是证明切线的常用方法.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )| A、30° | B、36° |
| C、50° | D、60° |
 如图,直线a与直线c相交于点O,则∠1的度数是( )
如图,直线a与直线c相交于点O,则∠1的度数是( )| A、60° | B、50° |
| C、40° | D、30° |
 如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.
如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长. 如图,∠AOB和∠COD都是直角,OE是OD的反向延长线.
如图,∠AOB和∠COD都是直角,OE是OD的反向延长线.