题目内容
在△AOB中,若OA=OB=2a,⊙O的半径R=a,问:AB与⊙O相切、相交、相离时,∠A的取值范围分别是多少?
考点:直线与圆的位置关系
专题:
分析:可以先求得相切时∠A为30°,再根据相交时O离AB越来越近,则∠A逐渐变小,相离时,O离AB越来越远,则∠A逐渐变大接近90°,可得出结论.
解答:解:(1)相切时,设切点为C,则OC=a,OA=OB=2a,∠OAC=30°,
(2)相交时,O距AB的距离越来越小,∠OAC越来越小,最终接近0°,
∠OAC的取值范围是:0°≤∠OAC≤30°,
(3)相离时,O距AB的距离越来越大,∠OAC越来越大,最终接近90°,
∠OAC的取值范围是:0°≤∠OAC≤90°.
(2)相交时,O距AB的距离越来越小,∠OAC越来越小,最终接近0°,
∠OAC的取值范围是:0°≤∠OAC≤30°,
(3)相离时,O距AB的距离越来越大,∠OAC越来越大,最终接近90°,
∠OAC的取值范围是:0°≤∠OAC≤90°.
点评:本题主要考查直线和圆的位置关系,利用条件求得相切时的∠A的大小是解题的关键.

练习册系列答案
相关题目
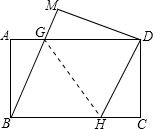 如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( )
如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( ) 如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.
如图,在△ABC中,∠C=90°∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.