题目内容
14.方程$\frac{x-1}{x+1}+\frac{4x}{{x}^{2}-1}=1$解的情况是无根.(填写“两个根”、“一个根”或“无根”)分析 先将分式方程化为整式方程,解整式方程并判断整式方程的解是否为分式方程的解即可.
解答 解:方程两边都乘(x+1)(x-1),可得
$\frac{x-1}{x+1}$×(x+1)(x-1)+$\frac{4x}{(x+1)(x-1)}$×(x+1)(x-1)=(x+1)(x-1),
即(x-1)2+4x=x2-1,
解得x=-1,
检验:当x=-1时,(x+1)(x-1)=0,
∴x=-1是原方程的增根,
∴原方程无解,
故答案为:无根.
点评 本题主要考查了分式方程的解,在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.

练习册系列答案
相关题目
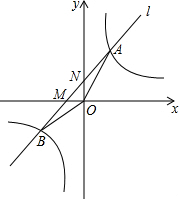 如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).
如图,设反比例函数的解析式为y=$\frac{3k}{x}$(k>0).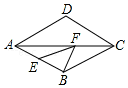 如图,在边长为10的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为5$\sqrt{3}$.
如图,在边长为10的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为5$\sqrt{3}$.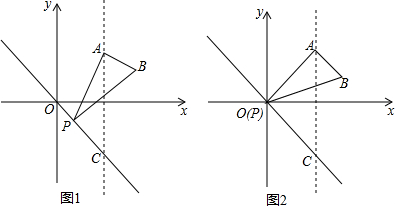
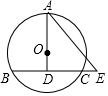 如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.
如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.