题目内容
16.先化简,再求值:$\frac{x-1}{{x}^{2}-9}$÷($\frac{x}{x-3}$-$\frac{5x-1}{{x}^{2}-9}$),其中x=3tan30°+$\sqrt{2}$cos45°.分析 先根据分式的混合运算顺序和法则化简原式,再由特殊锐角三角函数值求得x的值,代入即可求得答案.
解答 解:原式=$\frac{x-1}{(x+3)(x-3)}$÷[$\frac{x(x+3)}{(x+3)(x-3)}$-$\frac{5x-1}{(x+3)(x-3)}$]
=$\frac{x-1}{(x+3)(x-3)}$÷$\frac{{x}^{2}+3x-5x+1}{(x+3)(x-3)}$
=$\frac{x-1}{(x+3)(x-3)}$•$\frac{(x+3)(x-3)}{(x-1)^{2}}$
=$\frac{1}{x-1}$,
∵x=3tan30°+$\sqrt{2}$cos45°=3×$\frac{\sqrt{3}}{3}$+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=$\sqrt{3}$+1,
∴原式=$\frac{1}{\sqrt{3}+1-1}$=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查分式的化简求值和特殊锐角的三角函数值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.-2的倒数是( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
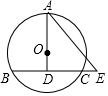 如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.
如图,⊙O的半径为5,弦BC=8,点A在⊙O上,AO⊥BC,垂足为D、E为BC延长线上一点,AE=10,则CE的长为2.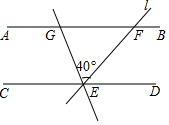 如图,AB∥CD,直线l与AB、CD相交于点E、F,将直线l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=60度.
如图,AB∥CD,直线l与AB、CD相交于点E、F,将直线l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=60度.