题目内容
一次函数y=kx+b的图象经过（2，0）（0，-2），则函数表达式为（ ）
| A、y=x-2 |
| B、y=-x+2 |
| C、y=2x-1 |
| D、y=2x+1 |
考点：待定系数法求一次函数解析式
专题：
分析：利用待定系数法把点（2，0），（0，-2）代入y=kx+b，可得关于k、b的方程组，再解出方程组可得k、b的值，进而得到函数解析式．
解答：解：∵一次函数y=kx+b的图象经过点（2，0），（0，-2）
∴
，
解得：
∴这个一次函数的表达式为y=x-2．
故应选A．
∴
|
解得：
|
∴这个一次函数的表达式为y=x-2．
故应选A．
点评：此题主要考查了待定系数法求一次函数解析式，一般步骤是：
（1）先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；
（2）将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；
（3）解方程或方程组，求出待定系数的值，进而写出函数解析式．
（1）先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；
（2）将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；
（3）解方程或方程组，求出待定系数的值，进而写出函数解析式．
练习册系列答案
阅读快车系列答案
相关题目
如果单项式-2xa+1y3与
x2yb是同类项，那么a，b的值分别为（ ）
| 1 |
| 2 |
| A、a=1，b=3 |
| B、a=1，b=2 |
| C、a=2，b=3 |
| D、a=2，b=2 |
把一个表面漆成绿色的正方体平均分成27个小正方体，并从中任取一个，恰好取到有三个侧面都是绿色的小正方体的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
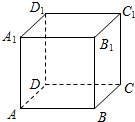如图，设正方体ABCD-A1B1C1D1的棱长为1，黑、白两个甲壳虫同时从A点出发，以相同的速度分别沿棱向前爬行，黑甲壳虫爬行的路线是AA1→A1D1→…，白甲壳虫爬行的路线是AB→BB1→…，并且都遵循如下规则：所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交（其中n是正整数）．那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时，它们之间的距离是（ ）下列各式对于任意数a都能成立的是（ ）
| A、7a＞6a | ||||
| B、a＞-a | ||||
C、
| ||||
| D、3-a＜4-a |
将矩形ABCD沿BE折叠，得到如图所示的图形，已知∠CBA′=34°，则∠AEB的大小是（ ）| A、34° | B、56° |
| C、28° | D、62° |