题目内容
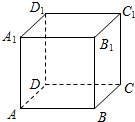 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )| A、0 | ||
| B、1 | ||
C、
| ||
D、
|
考点:勾股定理的应用
专题:
分析:先确定黑、白两个甲壳虫各爬行完第2008条棱分别停止的点,再根据勾股定理求出它们之间的位置.
解答: 解:连接CD1,
解:连接CD1,
因为2013÷6=335…3,所以黑、白两个甲壳虫各爬行完第2013条棱分别停止的点是D和A1,
由于∠DAA1=90°,
故选C.
 解:连接CD1,
解:连接CD1,因为2013÷6=335…3,所以黑、白两个甲壳虫各爬行完第2013条棱分别停止的点是D和A1,
由于∠DAA1=90°,
故选C.
点评:此题是一道趣味性题目,不仅考查了阅读理解能力,还考查了勾股定理在空间的应用,综合性较强.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
下列关系式中y是x的二次函数的是( )
A、y=
| ||
B、y=
| ||
C、y=
| ||
| D、y=ax2 |
计算的(-a)3•(-a)4结果是( )
| A、a7 |
| B、-a12 |
| C、a12 |
| D、-a7 |
计算(-0.25)2013×(-4)2014等于( )
| A、-1 | B、1 | C、-4 | D、4 |
一次函数y=kx+b的图象经过(2,0)(0,-2),则函数表达式为( )
| A、y=x-2 |
| B、y=-x+2 |
| C、y=2x-1 |
| D、y=2x+1 |
 如图,长方体的高为8cm,底面是正方形,边长为3cm,现有绳子从A出发,沿长方体表面到达C处,则绳子的最短长度是( )
如图,长方体的高为8cm,底面是正方形,边长为3cm,现有绳子从A出发,沿长方体表面到达C处,则绳子的最短长度是( )| A、8 | B、9 | C、10 | D、11 |
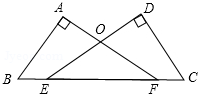 已知:如图,E是BC的中点,∠1=∠2,∠B=∠C.求证:AB=DC.
已知:如图,E是BC的中点,∠1=∠2,∠B=∠C.求证:AB=DC.