题目内容
 如图,∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动.当OC与OA成一直线时停止转动.
如图,∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动.当OC与OA成一直线时停止转动.(1)
(2)当OC与OD的夹角是30度时,求转动的时间是多少秒?
(3)若OB平分∠COD,求转动的时间是多少秒?并画出此时的OC与OD,写出图中∠AOD的余角.
考点:一元一次方程的应用,角平分线的定义,余角和补角
专题:几何动点问题
分析:(1)利用两射线转动的速度和方向以及利用∠AOB是直角,得出等式求出即可;
(2)利用两射线转动的速度和方向以及利用∠AOB是直角,得出等式求出即可;
(3)利用OB平分∠COD,进而得出等式求出即可.
(2)利用两射线转动的速度和方向以及利用∠AOB是直角,得出等式求出即可;
(3)利用OB平分∠COD,进而得出等式求出即可.
解答: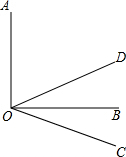 解:(1)∵∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动,
解:(1)∵∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动,
∴设x秒时,OC与OD重合,则8x+2x=90,
解得:x=9,
故答案为:9;
(2)设转动t秒时,OC与OD的夹角是30度
根据题意,得:
8t+2t=90-30或8t+2t=90+30
解得:t=6或t=12
答:当转动6秒或12秒时,OC与OD的夹角是30度.
(3)设转动m秒时,OB平分∠COD
则:8m-90=2m
解得:m=15
答:转动15秒时,OB平分∠COD.
此时,OC和OD的位置如右图,∠AOD的余角有∠BOD和∠BOC.
 解:(1)∵∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动,
解:(1)∵∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动,∴设x秒时,OC与OD重合,则8x+2x=90,
解得:x=9,
故答案为:9;
(2)设转动t秒时,OC与OD的夹角是30度
根据题意,得:
8t+2t=90-30或8t+2t=90+30
解得:t=6或t=12
答:当转动6秒或12秒时,OC与OD的夹角是30度.
(3)设转动m秒时,OB平分∠COD
则:8m-90=2m
解得:m=15
答:转动15秒时,OB平分∠COD.
此时,OC和OD的位置如右图,∠AOD的余角有∠BOD和∠BOC.
点评:此题主要考查了一元一次方程的应用以及角平分线的性质和余角的定义,正确根据题意得出等量关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,将△ABC绕顶点C旋转,点A转到BC边上的点E处,点B转到点F处,延长FE交AB于点D,则S△BED=( )
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,将△ABC绕顶点C旋转,点A转到BC边上的点E处,点B转到点F处,延长FE交AB于点D,则S△BED=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
关于单项式:-
,下列说法正确的是( )
| 2x2y |
| 5 |
| A、次数是2 | ||
| B、次数是3 | ||
| C、系数是-2 | ||
D、系数是
|
 如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是( )
如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是( )| A、3cm | B、4cm |
| C、5cm | D、6cm |
 已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
已知:如图,B、C是线段AD上两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=9cm,求线段MC的长.
 某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图.
某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图.