题目内容
2.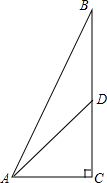 如图,在Rt△ABC中,∠C=90°,sinB=$\frac{5}{13}$,AD为中线,求sin∠CAD的值.
如图,在Rt△ABC中,∠C=90°,sinB=$\frac{5}{13}$,AD为中线,求sin∠CAD的值.
分析 在Rt△ABC中,∠C=90°,sinB=$\frac{5}{13}$,则设AC=5k,AB=13k,由勾股定理求得BC,进而求得CD的长,在直角△ACD中利用正弦的定义求解.
解答 解:在Rt△ABC中,∠C=90°,sinB=$\frac{5}{13}$,
设AC=5k,AB=13k,由勾股定理,得CB=12k.
∵AD为中线,
∴CD=6k.
则在Rt△ADC中,由勾股定理,得CB=$\sqrt{{5}^{2}+{6}^{2}}$=$\sqrt{61}$k,
∴sin∠CAD=$\frac{6k}{\sqrt{61}k}$=$\frac{6\sqrt{61}}{61}$.
点评 本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列各数:-(-2),-|-2|,(-2)2,-22,(-2)3,-23,负数个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
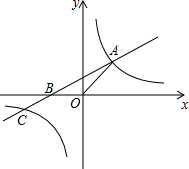 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=$\frac{4}{x}$交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=$\frac{4}{x}$交于点A、C,其中点A在第一象限,点C在第三象限.