题目内容
 已知:如图,AB=AC,AD∥BC,O是∠ABC和∠ACB平分线的交点,CO的延长线交AD于D.求证:DB⊥OB.
已知:如图,AB=AC,AD∥BC,O是∠ABC和∠ACB平分线的交点,CO的延长线交AD于D.求证:DB⊥OB.考点:等腰三角形的性质,平行线的性质
专题:证明题
分析:根据平行线的性质和角平分线的定义得到∠ADC=∠ACD,再根据等底对等腰得到AD=AC,从而得到AD=AB,再根据等腰对等底得到BD是∠ABF的平分线,再根据角平分线的性质即可求解.
解答:证明:∵AD∥BC,
∴∠ADC=∠BCD,
∵CO是∠ACB的平分线,
∴∠ACD=∠BCD,
∴∠ADC=∠ACD,
∴AD=AC,
∵AB=AC,
∴AB=AD,
∴∠ADB=∠ABD,
∵AD∥BC,
∴∠ADB=∠DBF,
∴∠ABD=∠DBF,
∵BO是∠ABC的平分线,
∴∠DBO=90°,
∴DB⊥OB.
∴∠ADC=∠BCD,
∵CO是∠ACB的平分线,
∴∠ACD=∠BCD,
∴∠ADC=∠ACD,
∴AD=AC,
∵AB=AC,
∴AB=AD,
∴∠ADB=∠ABD,
∵AD∥BC,
∴∠ADB=∠DBF,
∴∠ABD=∠DBF,
∵BO是∠ABC的平分线,
∴∠DBO=90°,
∴DB⊥OB.
点评:考查了平行线的性质和角平分线的定义,等底对等腰,等腰对等底的性质,关键是得到∠ABD=∠DBF.

练习册系列答案
相关题目
 如图,一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离是( )
如图,一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离是( )| A、4πr | B、2πr |
| C、πr | D、2r |




 如图,在房子外的屋檐E处装有一台监视器,房子前面有一面落地的广告牌.
如图,在房子外的屋檐E处装有一台监视器,房子前面有一面落地的广告牌.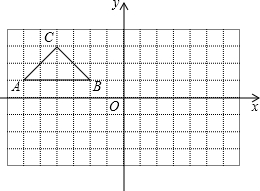 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: 画出下图中几何体的三种视图.
画出下图中几何体的三种视图.