题目内容
11.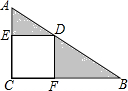 如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.(提示:将△AED绕D点按逆时针方向旋转90°,得到△A1FD,把阴影部分构造成规则的图形)
分析 根据正方形的性质得DE=DF,∠EDF=∠DFC=∠DEC=90°,则将△AED绕D点按逆时针方向旋转90°,得到△A1FD,根据旋转的性质得∠ADA′=90°,∠DEA=∠DFA′=90°,则可判断点A′在CF上,所以DA′=DA=3,然后利用阴影部分的面积等于Rt△DA′B的面积求解.
解答 解: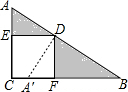 ∵四边形ECFD为正方形,
∵四边形ECFD为正方形,
∴DE=DF,∠EDF=∠DFC=∠DEC=90°,
∴将△AED绕D点按逆时针方向旋转90°,得到△A1FD,如图,
∴∠ADA′=90°,∠DEA=∠DFA′=90°,
∴点A′在CF上,DA′=DA=3,
∴S△DEA=S△DFA′,
∴阴影部分的面积=S△DA′B=$\frac{1}{2}$×3×4=6.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质.通过旋转把阴影部分构造成规则的图形是解决此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1.开封市某初中为了更好地开展“阳光体育一小时”活动,围绕着“你最喜欢的体育活动项目是什么(只写一项)?”的问题,对全校学生进行了随机抽样调查,以下是根据得到的相关数据绘制的统计图的一部分.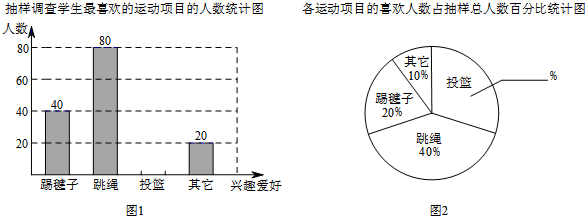
各年级人数统计表
请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校七年级学生比九年级学生少20人,请你补全上表,并利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?

各年级人数统计表
| 年级 | 七年级 | 八年级 | 九年级 |
| 学生人数 | 850 | 680 |
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校七年级学生比九年级学生少20人,请你补全上表,并利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?
16.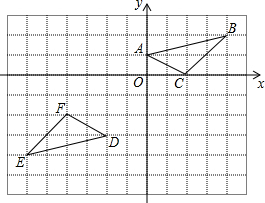 如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
 如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )| A. | (-1,0) | B. | (-1,-1) | C. | (-2,-1) | D. | (-2,0) |
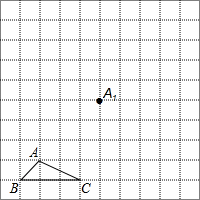 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).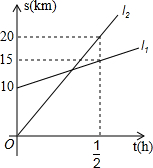 如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题:
如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题: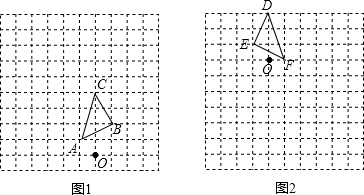
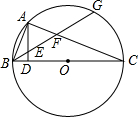 如图,BC是⊙O的直径,G为弧$\widehat{AC}$的中点,AD⊥BC于D,求证:AE=AF.
如图,BC是⊙O的直径,G为弧$\widehat{AC}$的中点,AD⊥BC于D,求证:AE=AF.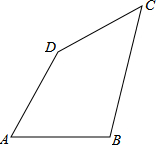 如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积.
如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积.