题目内容
3.先化简,再求代数式(1-$\frac{3}{x+2}$)÷$\frac{{x}^{2}-1}{x+2}$的值,其中x=4sin45°-2cos60°.分析 先化简原式以及x,然后将x的值代入原式即可求出答案.
解答 解:当x=4×$\frac{\sqrt{2}}{2}$-2×$\frac{1}{2}$=2$\sqrt{2}$-1时,
∴原式=$\frac{x-1}{x+2}$×$\frac{x+2}{(x+1)(x-1)}$
=$\frac{1}{x+1}$
=$\frac{1}{2\sqrt{2}}$
=$\frac{\sqrt{2}}{4}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )| A. | (-4,-1) | B. | (-1,-4) | C. | (5,-4) | D. | (-5,-4) |
14.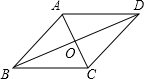 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )| A. | AB=AD | B. | AC=BD | C. | BD平分∠ABC | D. | AC⊥BD |
11.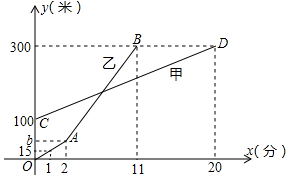 甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
 甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )| A. | 165m | B. | 160m | C. | 135m | D. | 120m |
18.计算:(1)$\frac{3}{4}\sqrt{3\frac{3}{4}}×(-18\sqrt{45})$;(2)$\sqrt{2x-3y}•\sqrt{4{x}^{2}-9{y}^{2}}$.
4.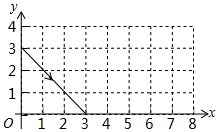 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )| A. | (3,0) | B. | (0,3) | C. | (1,4) | D. | (8,3) |