题目内容
7. 已知如图,⊙P与x轴切于点O,P点的坐标为(0,2),点A在⊙P上,且A点的坐标为(1,2+$\sqrt{3}$),⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为($\frac{5}{3}π$,2)(结果保留π)
已知如图,⊙P与x轴切于点O,P点的坐标为(0,2),点A在⊙P上,且A点的坐标为(1,2+$\sqrt{3}$),⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为($\frac{5}{3}π$,2)(结果保留π)
分析 过点A,作AB⊥y轴于点B,AC⊥x轴于点C,由点A的坐标,可求出∠APB的度数,进而可得到∠APO的度数,再根据点P的横坐标是A转过的长度,纵坐标是2,由弧长公式即可求解.
解答 解: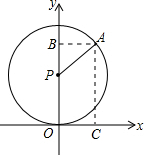 过点A,作AB⊥y轴于点B,AC⊥x轴于点C,易得四边形ABOC是矩形,
过点A,作AB⊥y轴于点B,AC⊥x轴于点C,易得四边形ABOC是矩形,
∴AC=BO,AB=OC,
∵A点的坐标为(1,2+$\sqrt{3}$),⊙P的半径是2,
∴AB=OC=1,BP=AC-OP=2+$\sqrt{3}$-2=$\sqrt{3}$,
∴tan∠APB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$
∴∠APB=30°,
∴∠APO=150°,
∴A转过的长度=$\frac{150×π×2}{180}$=$\frac{5}{3}π$,
即点P的坐标是($\frac{5}{3}π$,2).
故答案为($\frac{5}{3}π$,2).
点评 本题主要考查了切线的性质,坐标与图形的关系,弧长公式的计算,掌握公式是解题的关键.

练习册系列答案
相关题目
16.已知关于x的方程5x-2m=4x-6m+1,若该方程的解比1大,则m的值可能为( )
| A. | 4 | B. | 1 | C. | 0 | D. | -3 |
17.一艘轮船在两个码头间航行,顺水航行60km所需时间与逆水航行48km所需时间相同,已知船在静水中的速度为18km/h.若设水流速度为xkm/h,则列出的方程正确的是( )
| A. | $\frac{60}{x+18}$=$\frac{48}{x-18}$ | B. | $\frac{60}{18-x}$=$\frac{48}{18+x}$ | C. | $\frac{60}{18+x}$=$\frac{48}{18-x}$ | D. | 60(18+x)=48(x-18) |
 如图,△ABO为等腰直角三角形,A(-4,0),直角顶点B在第二象限.点C在y轴上移动,以BC为斜边作等腰直角△BCD,我们发现直角顶点D点随着C点的移动也在一条直线上移动,这条直线的函数表达式是y=x+2或y=-x+2.
如图,△ABO为等腰直角三角形,A(-4,0),直角顶点B在第二象限.点C在y轴上移动,以BC为斜边作等腰直角△BCD,我们发现直角顶点D点随着C点的移动也在一条直线上移动,这条直线的函数表达式是y=x+2或y=-x+2.