题目内容
17.一艘轮船在两个码头间航行,顺水航行60km所需时间与逆水航行48km所需时间相同,已知船在静水中的速度为18km/h.若设水流速度为xkm/h,则列出的方程正确的是( )| A. | $\frac{60}{x+18}$=$\frac{48}{x-18}$ | B. | $\frac{60}{18-x}$=$\frac{48}{18+x}$ | C. | $\frac{60}{18+x}$=$\frac{48}{18-x}$ | D. | 60(18+x)=48(x-18) |
分析 顺水速度=水流速度+静水速度,逆水速度=静水速度-水流速度.根据“顺水航行60km所需时间与逆水航行48km所需时间相同”可列出方程.
解答 解:设水流速度为xkm/h,根据题意得:
$\frac{60}{18+x}=\frac{48}{18-x}$,
故选C
点评 此题考查了分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.本题需注意顺流速度与逆流速度的求法.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
12.下列命题中,真命题是( )
| A. | 内错角相等 | B. | 一个正数有2个平方根 | ||
| C. | 立方根等于本身的数是1和0 | D. | 若a>b,则-a>-b |
7.甲乙两人练习赛跑,甲每秒跑7米,乙每秒跑6.5米,甲让乙先跑5米,设x秒后,甲可以追上乙,则下列方程不正确结果是( )
| A. | 7x=6.5x+5 | B. | 7x-5=6.5 | C. | (7-6.5)x=5 | D. | 6.5x=7x-5 |
 已知如图,⊙P与x轴切于点O,P点的坐标为(0,2),点A在⊙P上,且A点的坐标为(1,2+$\sqrt{3}$),⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为($\frac{5}{3}π$,2)(结果保留π)
已知如图,⊙P与x轴切于点O,P点的坐标为(0,2),点A在⊙P上,且A点的坐标为(1,2+$\sqrt{3}$),⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为($\frac{5}{3}π$,2)(结果保留π)
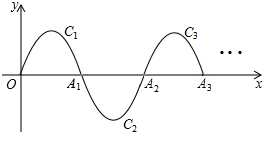 一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…若P(2015,m)是其中某段抛物线上一点,则m=-2.
一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…若P(2015,m)是其中某段抛物线上一点,则m=-2.