Question

12．如图，△ABO为等腰直角三角形，A（-4，0），直角顶点B在第二象限．点C在y轴上移动，以BC为斜边作等腰直角△BCD，我们发现直角顶点D点随着C点的移动也在一条直线上移动，这条直线的函数表达式是y=x+2或y=-x+2．

Answer 1

分析 抓住两个特殊位置：当BC与x轴平行时，求出D的坐标；C与原点重合时，D在y轴上，求出此时D的坐标，设所求直线解析式为y=kx+b，将两位置D坐标代入得到关于k与b的方程组，求出方程组的解得到k与b的值，即可确定出所求直线解析式．

解答 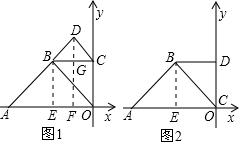解：当BC与x轴平行时，过B作BE⊥x轴，过D作DF⊥x轴，交BC于点G，如图1所示，
∵等腰直角△ABO的O点是坐标原点，A的坐标是（-4，0），
∴AO=4，
∴BC=BE=AE=EO=GF=$\frac{1}{2}$OA=2，OF=DG=BG=CG=$\frac{1}{2}$BC=1，DF=DG+GF=3，
∴D坐标为（-1，3）；
当C与原点O重合时，D在y轴上，
此时OD=BE=2，即D（0，2），
设所求直线解析式为y=kx+b（k≠0），
将两点坐标代入得：$\left\{\begin{array}{l}{-k+b=3}\\{b=2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$．
则这条直线解析式为y=-x+2，
当D（-1，1）和D（-2，0）
于是得到y=x+2，
综上所述：这条直线的函数表达式是y=x+2或y=-x+2．
故答案为：y=x+2或y=-x+2．

点评 本题考查了轨迹问题，待定系数法确定一次函数解析式，等腰直角三角形的性质，坐标与图形性质，熟练运用待定系数法是解本题的关键．