题目内容
 一胡同拐角处的俯视图如图所示,已知墙壁AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的宽度都为2m,内壁EF是半径为1m的四分之一圆弧,DE、FG分别与弧EF相切于E、F两点.现有户人家正在装修,需要买一些长方形木板,那么当木板的宽度不超过
一胡同拐角处的俯视图如图所示,已知墙壁AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的宽度都为2m,内壁EF是半径为1m的四分之一圆弧,DE、FG分别与弧EF相切于E、F两点.现有户人家正在装修,需要买一些长方形木板,那么当木板的宽度不超过考点:切线的性质
专题:应用题
分析:连结OE并延长交AB于M,连结OF并延长交BC于N,连结OB、MN,OB交弧EF于P点,根据切线的性质得OF⊥GF,OE⊥DE,OE=OF=1,则ON⊥BC,OM⊥AB,加上OM=ON=3,可判断四边形BMON为正方形,所以OB=
OM=3
,则BP=OB-OP=3
-1,过点P作弧EF的切线分别交AB、BC于Q、R,则QR为木板的最大宽度,利用直角三角形斜边上的中线性质得BP=
QR,即QR=2BP=(6
-2)m.
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
解答: 解:连结OE并延长交AB于M,连结OF并延长交BC于N,连结OB、MN,OB交弧EF于P点,
解:连结OE并延长交AB于M,连结OF并延长交BC于N,连结OB、MN,OB交弧EF于P点,
∵DE、FG分别与弧EF相切于E、F两点,
∴OF⊥GF,OE⊥DE,OE=OF=1,
∴ON⊥BC,OM⊥AB,
∴四边形BMON为矩形,
而OM=ON=1+2=3,
∴四边形BMON为正方形,
∴OB=
OM=3
,
∴BP=OB-OP=3
-1,
过点P作弧EF的切线分别交AB、BC于Q、R,则QR为木板的最大宽度,
∵点P为弧EF的中点,
∴BP=
QR,
∴QR=2BP=2(3
-1)=(6
-2)m,
即当木板的宽度不超过(6
-2)m时,才能顺利通过此胡同.
故答案为(6
-2).
 解:连结OE并延长交AB于M,连结OF并延长交BC于N,连结OB、MN,OB交弧EF于P点,
解:连结OE并延长交AB于M,连结OF并延长交BC于N,连结OB、MN,OB交弧EF于P点,∵DE、FG分别与弧EF相切于E、F两点,
∴OF⊥GF,OE⊥DE,OE=OF=1,
∴ON⊥BC,OM⊥AB,
∴四边形BMON为矩形,
而OM=ON=1+2=3,
∴四边形BMON为正方形,
∴OB=
| 2 |
| 2 |
∴BP=OB-OP=3
| 2 |
过点P作弧EF的切线分别交AB、BC于Q、R,则QR为木板的最大宽度,
∵点P为弧EF的中点,
∴BP=
| 1 |
| 2 |
∴QR=2BP=2(3
| 2 |
| 2 |
即当木板的宽度不超过(6
| 2 |
故答案为(6
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
 如图,Rt△ABC中,∠ACB=90°,CD丄AB于D.
如图,Rt△ABC中,∠ACB=90°,CD丄AB于D. 如图所示,一辆卡车装满货物后,高4cm,宽3cm,这辆卡车能通过横截面如图(上方为半圆)的隧道吗?为什么?
如图所示,一辆卡车装满货物后,高4cm,宽3cm,这辆卡车能通过横截面如图(上方为半圆)的隧道吗?为什么?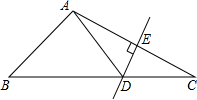 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是
如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是 二次函数y=-2x2+4x的对称轴是x=
二次函数y=-2x2+4x的对称轴是x=