题目内容
14.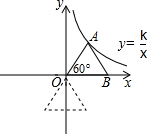 已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.
已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.
分析 依题意,旋转后,B、O、A三点在同一直线上,根据双曲线的中心对称性可知OA=OB,又∠AOB=60°,可知△AOB为等边三角形,过A点作x轴的垂线,解直角三角形求A点的坐标即可求k的值.
解答 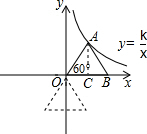 解:过A点作AC⊥x轴,垂足为C,
解:过A点作AC⊥x轴,垂足为C,
设旋转后点B的对应点为B′,则∠AOB′=∠AOB+∠BOB′=60°+120°=180°,
∵双曲线是中心对称图形,
∴OA=OB′,即OA=OB,
又∵∠AOB=60°,
∴△AOB为等边三角形,OA=AB=6,
在Rt△AOC中,OC=OA×cos60°=3,
AC=OA×sin60°=3$\sqrt{3}$,
∴k=OC×AC=9$\sqrt{3}$.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数的增减性是解答此题的关键.

练习册系列答案
相关题目
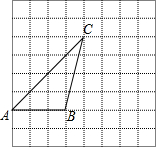 如图,△ABC的顶点A,B,C都在格点上,根据要求完成下列任务:
如图,△ABC的顶点A,B,C都在格点上,根据要求完成下列任务: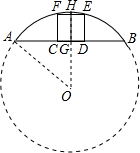 如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.
如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.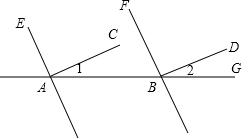 如图,已知AC⊥AE,BD⊥BF,∠1=∠2=35°,证明:AC∥BD,AE∥BF.
如图,已知AC⊥AE,BD⊥BF,∠1=∠2=35°,证明:AC∥BD,AE∥BF.