题目内容
19.若m为整数,关于x的方程x2-mx+$\frac{1}{2}$m+1=0的根是有理数,求m.分析 首先利用根的判别式得出△=m2-2m-4,再进一步利用完全平方数的性质探讨得出答案即可.
解答 解:△=m2-2m-4,
∵根为有理数,
∴△必为完全平方数,
也可根据x=$\frac{m±\sqrt{△}}{2×1}$,
则没m2-2m-4=k2(k≥0)
m2-2m-4-k2=0
m2-2m+1-k2=5
(m-1)2-k2=5
(m-1+k)(m-1-k)=5
∵m,k为整数,且k≥0,
则$\left\{\begin{array}{l}{m-1+k=1}\\{m-1-k=5}\end{array}\right.$ 或$\left\{\begin{array}{l}{m-1+k=5}\\{m-1-k=1}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=4}\\{k=-2(不合题意)}\end{array}\right.$ $\left\{\begin{array}{l}{m=4}\\{k=2}\end{array}\right.$
∴m=4时,根为有理数.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

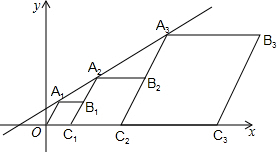 菱形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按照如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上.已知∠A1OC1=60°,点B1(3,$\sqrt{3}$),B2(8,2$\sqrt{3}$),则An的坐标是(3•2n-1-2,2n-1•$\sqrt{3}$)(用含n的式子表示)
菱形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按照如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上.已知∠A1OC1=60°,点B1(3,$\sqrt{3}$),B2(8,2$\sqrt{3}$),则An的坐标是(3•2n-1-2,2n-1•$\sqrt{3}$)(用含n的式子表示)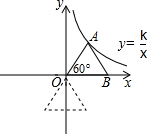 已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.
已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.