题目内容
15. 在Rt△ABC中,DE⊥AB于D,AD=2,AB=8,BC=6,求AE的长.
在Rt△ABC中,DE⊥AB于D,AD=2,AB=8,BC=6,求AE的长.
分析 由勾股定理求出AC,证明△ADE∽△ABC,得出$\frac{AE}{AC}=\frac{AD}{AB}$=$\frac{1}{4}$,求出AE=$\frac{1}{4}$AC=$\frac{5}{2}$即可.
解答 解:∵在Rt△ABC中,DE⊥AB于D,AB=8,BC=6,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}=\frac{AD}{AB}$=$\frac{2}{8}$=$\frac{1}{4}$,
∴AE=$\frac{1}{4}$AC=$\frac{5}{2}$.
点评 本题考查了相似三角形的判定与性质、勾股定理;熟练掌握勾股定理,证明三角形相似是解决问题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.我们知道,在弹性限度内,弹簧挂上重物后会伸长.已知一根弹簧的长度(cm)与所挂重物的质量(kg)之间的关系如下表,则下列说法错误的是( )
| 重物的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
| A. | 在这一变化过程中,重物的质量是自变量,弹簧的长度是因变量 | |
| B. | 当所挂重物的质量是4kg时,弹簧的长度是14cm | |
| C. | 在弹性限度内,当所挂重物的质量是6kg时,弹簧的长度是16cm | |
| D. | 当不挂重物时,弹簧的长度应为12cm |
6.对角线互相垂直平分的四边形是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 任意四边形 |
7. 如图,在△ABC中,BC边上的高是( )
如图,在△ABC中,BC边上的高是( )
 如图,在△ABC中,BC边上的高是( )
如图,在△ABC中,BC边上的高是( )| A. | CE | B. | AD | C. | CF | D. | AB |
 如图,在△ABC中,AD、BE分别是边BC、AC的高,点F是AB边的中点.
如图,在△ABC中,AD、BE分别是边BC、AC的高,点F是AB边的中点.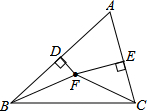 如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.
如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.