题目内容

如图，用两根等长的金属丝，各自首尾相接，分别围成正方形ABCD和扇形A1D1C1，使A1D1=AD，D1C1=DC，正方形面积为P，扇形面积为Q，那么P和Q的关系是（　　）
A、P＜QB、P=Q
C、P＞QD、无法确定
考点：扇形面积的计算,正方形的性质
专题：
分析：先求出正方形的面积P，然后利用扇形的面积公式求出Q，然后比较两者的大小关系即可．
解答：解：正方形面积P=AB2，扇形面积Q=
1
2
lr=
1
2
×2AB•AB=AB2，
其中l为扇形弧长，等于正方形2个边长，r为扇形半径，等于正方形边长，
则P=Q．
故选B．
点评：本题主要考查了函数模型的选择与应用，同时考查了扇形面积的度量，属于中档题．
练习册系列答案
相关题目
如图1，线段AB=20cm，点P沿线段AB自A点向B点以2cm/s的速度运动，同时点Q沿线段BA自点B向点A以3cm/s的速度运动．
（1）当点P、Q相遇时，点P与点B的距离是多少？
（2）如图2，AO=PO=OC=2cm，∠POQ=60°，现点P绕着点O以30°/s的速度顺时针旋转（一周后停止），同时点Q沿直线BA自点B向A运动，假设P、Q两点也能相遇，求点Q运动的速度．
已知抛物线y=-x2-2x+3与x轴交于A（-3，0），B（1，0）两点，与y轴交于点C（0，3），将直线BC向下平移，与抛物线交于点B′，C′（B′与B对应，C′与C对应），与y轴交于点D，当点D是线段B′C′的三等分点时，求点D的坐标．
已知如图AC=CD=DB，AC=2AM，BN=
1
2
BM，如果MN=5cm，求AB、CN的长．
已知：如图，∠AOB=80°，ON是∠AOC的平分线，OM是∠BOC的平分线．
（1）当∠AOC=30°时，求∠MON的大小；
（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？请说明理由．
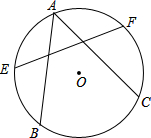已知：⊙O中弦AB、AC，且∠BAC=60°，E、F分别为
AB
、
AC
中点，连EF交AB、AC于G、H．求证：GH2=GE•HF．
如图，将△ABC沿BC方向平移得到△DEF，△ABC与△DEF重叠部分（图中阴影部分）的面积是△ABC的一半．已知BC=2，求△ABC平移的距离．
如图，如果用（0，0）表示旗杆的位置，用（-8，0）表示校门的位置，则图书馆的位置用这种方式表示为
 
．
如果9x2+kx+25是一个完全平方式，那么k的值是（　　）
A、30B、±30
C、15D、±15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网