题目内容
如图1,线段AB=20cm,点P沿线段AB自A点向B点以2cm/s的速度运动,同时点Q沿线段BA自点B向点A以3cm/s的速度运动.
(1)当点P、Q相遇时,点P与点B的距离是多少?
(2)如图2,AO=PO=OC=2cm,∠POQ=60°,现点P绕着点O以30°/s的速度顺时针旋转(一周后停止),同时点Q沿直线BA自点B向A运动,假设P、Q两点也能相遇,求点Q运动的速度.

(1)当点P、Q相遇时,点P与点B的距离是多少?
(2)如图2,AO=PO=OC=2cm,∠POQ=60°,现点P绕着点O以30°/s的速度顺时针旋转(一周后停止),同时点Q沿直线BA自点B向A运动,假设P、Q两点也能相遇,求点Q运动的速度.

考点:一元一次方程的应用,数轴
专题:几何动点问题
分析:(1)根据相遇时,点P和点Q的运动的路程和等于AB的长列方程即可求解;
(2)由于点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
(2)由于点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
解答:解:(1)设经过ts后,点P、Q相遇.
依题意,有2t+3t=20,
解得,t=4,
点P与点B的距离是:AB-AP=20-2×4=12(cm).
答:当点P、Q相遇时,点P与点B的距离是12cm;
(2)点P,Q只能在直线AB上相遇,
则点P旋转到直线AB上的时间为
=2s,或
=8s.
设点Q的速度为ycm/s,
则有2y=20-4,解得y=8;
或8y=20,解得y=2.5.
答:点Q的速度为8cm/s或2.5cm/s.
依题意,有2t+3t=20,
解得,t=4,
点P与点B的距离是:AB-AP=20-2×4=12(cm).
答:当点P、Q相遇时,点P与点B的距离是12cm;
(2)点P,Q只能在直线AB上相遇,
则点P旋转到直线AB上的时间为
| 60 |
| 30 |
| 60+180 |
| 30 |
设点Q的速度为ycm/s,
则有2y=20-4,解得y=8;
或8y=20,解得y=2.5.
答:点Q的速度为8cm/s或2.5cm/s.
点评:此题考查的是一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
已知a=1-
,b=1-
,用a表示c的代数式为( )
| 1 |
| b |
| 1 |
| c |
A、c=
| ||
B、a=
| ||
C、c=
| ||
D、c=
|
如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,D1C1=DC,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )


| A、P<Q | B、P=Q |
| C、P>Q | D、无法确定 |
 如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.
如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.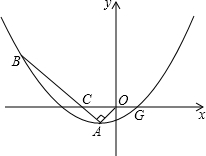 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).