题目内容
已知抛物线y=-x2-2x+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,3),将直线BC向下平移,与抛物线交于点B′,C′(B′与B对应,C′与C对应),与y轴交于点D,当点D是线段B′C′的三等分点时,求点D的坐标.
考点:抛物线与x轴的交点
专题:
分析:根据题意求出直线BC的解析式,进而得出直线B′C′为:y=3x+b,再利用根与系数的关系以及两点之间的距离关系得出答案.
解答: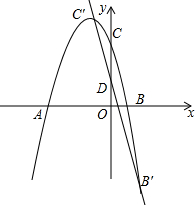 解:∵设直线BC的解析式为:y=kx+a,将(1,0),(0,3)代入得出:
解:∵设直线BC的解析式为:y=kx+a,将(1,0),(0,3)代入得出:
,
解得:
,
故直线BC的解析式为:y=-3x+3,
设直线B′C′为:y=3x+b,C′(x1,y1),B′(x2,y2),
由
,
故x2-x+b-3=0,
则x1+x2=1,x1x2=b-3,
由题意可得:
=
,
则x2=-2x1,故x1=-1,x2=2,-2=b-3,
解得:b=1,
故D(0,1).
 解:∵设直线BC的解析式为:y=kx+a,将(1,0),(0,3)代入得出:
解:∵设直线BC的解析式为:y=kx+a,将(1,0),(0,3)代入得出:
|
解得:
|
故直线BC的解析式为:y=-3x+3,
设直线B′C′为:y=3x+b,C′(x1,y1),B′(x2,y2),
由
|
故x2-x+b-3=0,
则x1+x2=1,x1x2=b-3,
由题意可得:
| 0-x1 |
| x2-0 |
| 1 |
| 2 |
则x2=-2x1,故x1=-1,x2=2,-2=b-3,
解得:b=1,
故D(0,1).
点评:此题主要考查了抛物线与x轴交点以及待定系数法求一次函数解析式,熟练利用根与系数的关系得出是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知a=1-
,b=1-
,用a表示c的代数式为( )
| 1 |
| b |
| 1 |
| c |
A、c=
| ||
B、a=
| ||
C、c=
| ||
D、c=
|
如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,D1C1=DC,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )


| A、P<Q | B、P=Q |
| C、P>Q | D、无法确定 |
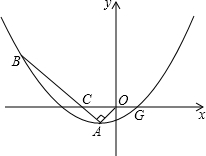 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).
 如图,a个半圆弧依次相外切,他们的圆心都在x轴的正半轴上,并都与直线y=
如图,a个半圆弧依次相外切,他们的圆心都在x轴的正半轴上,并都与直线y=