题目内容
5.下面说法正确的是( )| A. | 一个袋子里有100个同样质地的球,小华摸了8次球,每次都只摸到黑球,这说明袋子里面只有黑球 | |
| B. | 某事件发生的概率为0.5,也就是说,在两次重复的试验中必有一次发生 | |
| C. | 随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率为$\frac{1}{3}$ | |
| D. | 某校九年级有400名学生,一定有2名学生同一天过生日 |
分析 大量反复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值,而不是一种必然的结果,可得答案.
解答 解:A、一个袋子里有100个同样质地的球,小华摸了8次球,每次都只摸到黑球,这说明袋子里面黑球多,故A错误;
B、某事件发生的概率为0.5,也就是说,在两次重复的试验中可能发生两次,可能发生一次,可能不发生,故B错误;
C、随机掷一枚均匀的硬币两次,可能两次正面朝上,可能一次正面朝上,可能0次正面朝上,故C错误;
D、某校九年级有400名学生,一定有2名学生同一天过生日,故D正确;
故选:D.
点评 考查利用频率估计概率.大量反复试验下频率稳定值即概率.注意随机事件发生的概率在0和1之间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列函数中,自变量x的取值范围是x≥-3的是( )
| A. | y=$\sqrt{x+3}$ | B. | y=($\sqrt{x-3}$)2 | C. | y=$\frac{1}{x+3}$ | D. | y=$\sqrt{(x+3)^{2}}$ |
20. 如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )
如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )
 如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )
如图,l1∥l2,若∠1=100°,∠2=160°,则∠3为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
10.m,n 为正整数且3m×3n=81,则m,n值可能有( )
| A. | 7组 | B. | 6组 | C. | 5组 | D. | 3组 |
17.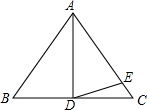 如图,在△ABC中,AB=AC,AD是边BC上的高,E为AC边上一点,且有AE=AD,∠EDC=22°,则∠B的度数为( )
如图,在△ABC中,AB=AC,AD是边BC上的高,E为AC边上一点,且有AE=AD,∠EDC=22°,则∠B的度数为( )
 如图,在△ABC中,AB=AC,AD是边BC上的高,E为AC边上一点,且有AE=AD,∠EDC=22°,则∠B的度数为( )
如图,在△ABC中,AB=AC,AD是边BC上的高,E为AC边上一点,且有AE=AD,∠EDC=22°,则∠B的度数为( )| A. | 44° | B. | 46° | C. | 56° | D. | 54° |
15.若x2+k+$\frac{1}{4}$mx是一个完全平方式,则k=( )
| A. | $\frac{1}{4}{m^2}$ | B. | $\frac{1}{8}{m^2}$ | C. | $\frac{1}{16}{m^2}$ | D. | $\frac{1}{64}{m^2}$ |
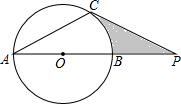 已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.