题目内容
13.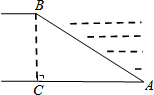 河堤的横断面如图所示,迎水坡AB=10米,迎水坡AB的坡比$1:\sqrt{3}$(坡比是坡面的垂直高度与水平宽度之比),则AC的长是( )
河堤的横断面如图所示,迎水坡AB=10米,迎水坡AB的坡比$1:\sqrt{3}$(坡比是坡面的垂直高度与水平宽度之比),则AC的长是( )| A. | 5米 | B. | $5\sqrt{3}$米 | C. | $\frac{{5\sqrt{3}}}{3}$米 | D. | $\frac{{10\sqrt{3}}}{3}$米 |
分析 根据迎水坡AB的坡比$1:\sqrt{3}$,设BC=x,AC=$\sqrt{3}$x,然后根据迎水坡AB=10米,利用勾股定理求出x的值,即可求解.
解答 解:∵AB的坡比$1:\sqrt{3}$,
∴设BC=x,AC=$\sqrt{3}$x,
则x2+($\sqrt{3}$x)2=100,
解得:x=5,
则AC=$\sqrt{3}$x=5$\sqrt{3}$.
故选B.
点评 本题考查了根据坡度和坡角解直角三角形的知识,解答本题的关键是根据坡比设出各边的长度,然后根据勾股定理求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列图形中是中心对称的是( )
| A. |  | B. |  | C. |  | D. |  |
3.计算:$\sqrt{\frac{5}{3}}$÷$\sqrt{\frac{1}{3}}$的结果是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 5 | D. | $\frac{\sqrt{5}}{3}$ |
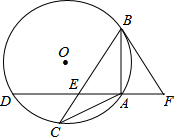 如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.
如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.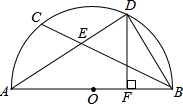 如图,AB为半圆O的直径,D为$\widehat{BC}$的中点,连结BC交AD于点E,DF⊥AB于F,$tanA=\frac{3}{4}$,DF=16,求DE的长?
如图,AB为半圆O的直径,D为$\widehat{BC}$的中点,连结BC交AD于点E,DF⊥AB于F,$tanA=\frac{3}{4}$,DF=16,求DE的长?