题目内容
17.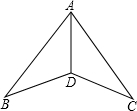 如图,峰峰先在一家白纸上用直尺画出了相等的线段AB和AC,然后用量角器作出了度数都为30°的∠ABD和∠ACD,最后连接AD,此时他就断定AD是∠BAC的平分线,你同意他的结论吗?如果同意,请证明;如果不同意,请说明理由.
如图,峰峰先在一家白纸上用直尺画出了相等的线段AB和AC,然后用量角器作出了度数都为30°的∠ABD和∠ACD,最后连接AD,此时他就断定AD是∠BAC的平分线,你同意他的结论吗?如果同意,请证明;如果不同意,请说明理由.
分析 连接BC,由AB=AC得到∠ABC=∠ACB,已知∠ABD=∠ACD,从而得出∠DBC=∠DCB,即BD=CD,又因为AB=AC,AD=AD,利用SSS判定△ABD≌△ACD,全等三角形的对应角相等即∠BAD=∠CAD,所以AD是∠BAC的平分线.
解答 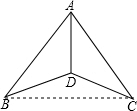 证明:连接BC,
证明:连接BC,
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABD=∠ACD,
∴∠DBC=∠DCB.
∴BD=CD.
在△ADB和△ADC中,$\left\{\begin{array}{l}{BD=CD}\\{AB=AC}\\{AD=AD}\end{array}\right.$,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD,
即AD是∠BAC的平分线.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:防止本题直接应用SSA,作出辅助线是解决本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
8.某帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共11千顶,“芦山地震”发生后,灾区A、B急需帐篷20千顶,该集团决定在一周内赶制出这批帐篷.总厂和分厂的生产效率分别比原来提高了100%和50%,恰好按时完成了这项任务.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的A,B两地,由于甲、乙两市通住A,B两地的情况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数和两地所急需的帐篷数如表:
请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的A,B两地,由于甲、乙两市通住A,B两地的情况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数和两地所急需的帐篷数如表:
| A地 | B地 | ||
| 每千顶帐篷 所需车辆数(单位:辆) | 甲市 | 4 | 7 |
| 乙市 | 3 | 5 | |
| 急需帐篷数(单位:千顶) | 9 | 11 | |
5.在下列数:-(-$\frac{1}{2}$),-|-9|,$\frac{22}{7}$,7,0中,正数有a个,负数有b个,整数有c个,负整数有d个,则a+b+c+d的值为( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
9.①要调查一批灯泡的使用寿命,②要对“神州十号”飞船零件质量进行检查,应采用( )
| A. | 都是普查 | B. | 都是抽查 | C. | ①是普查②是抽查 | D. | ①是抽查②是普查 |
6.下列各式从左到右的变形一定正确的是( )
| A. | $\frac{2}{3}$=$\frac{2a}{3a}$ | B. | $\frac{3a}{3b}$=$\frac{a}{b}$ | C. | $\frac{a}{b}$=$\frac{a+1}{b+1}$ | D. | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ |
7.已知m+n=2,mn=-2,则(2-m)(2-n)的值为( )
| A. | 2 | B. | -2 | C. | 0 | D. | 3 |
