题目内容
16.如图在平面直角坐标系中,点A(-2,4)在直线y=-x+b上,点E是直线y=-x+b与y轴的交点.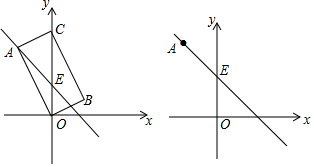
(1)求点E的坐标;
(2)若矩形AOBC的顶点C恰好在y轴上,求点C和点B的坐标;
(3)若点P是直线AE上的一个动点,在坐标平面内是否存在点Q,使以O、E、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
分析 (1)利用待定系数法求出直线AE的解析式,进而得出点E的坐标;
(2)根据矩形的性质,即可得出结论;
(3)分OE是菱形的边和对角线,利用菱形的性质即可得出结论.
解答 解:∵点A(-2,4)在直线y=-x+b上,
∴4=2+b,
∴b=2,
∴直线AE的解析式为y=-x+2,
∴E(0,2);
(2)∵A(-2,4),∴直线OA的解析式为y=-2x
∵四边形OACB是矩形,
∴AC⊥OA,
∴直线AC的解析式为y=$\frac{1}{2}$x+5,
∴C(0,5),同理:B(2,1);
(3)存在,理由:
∵E(0,2),
∴OE=2,
∵以O、E、P、Q为顶点的四边形是菱形,
∴①当OE为菱形的边时,PQ∥OE,PQ=OE=2,PE=2,
设P(m,-m+2),
∵E(0,2),
∴PE=$\sqrt{{m}^{2}+(-m+2-2)^{2}}$=$\sqrt{2}$|m|=2,
∴m=±$\sqrt{2}$,
∴P(-$\sqrt{2}$,$\sqrt{2}$+2)或($\sqrt{2}$,-$\sqrt{2}$+2),
∴Q(-$\sqrt{2}$,$\sqrt{2}$)或($\sqrt{2}$,-$\sqrt{2}$),
②当OE是菱形对角线时,点P,Q在OE的垂直平分线上,
∴点P,Q的纵坐标都为1,
∵P在直线AE上,
∴P(1,1),
∴Q(-1,1),
即:符合题意的点Q(-1,1)、(-$\sqrt{2}$,$\sqrt{2}$)或($\sqrt{2}$,-$\sqrt{2}$).
点评 此题是一次函数综合题,主要考查了菱形的性质,待定系数法,矩形的性质,解(1)的关键是利用待定系数法求出直线AE的解析式式,解(2)的关键是利用矩形的性质得出矩形的对边平行,邻边垂直,解(3)的关键是分OE是菱形的边和对角线两种情况讨论计算.

| A. | $\frac{2}{3}$=$\frac{2a}{3a}$ | B. | $\frac{3a}{3b}$=$\frac{a}{b}$ | C. | $\frac{a}{b}$=$\frac{a+1}{b+1}$ | D. | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ |
| A. | 2 | B. | -2 | C. | 0 | D. | 3 |
| A. | 2 | B. | -3 | C. | 3 | D. | 以上都不对 |
| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |
31-30=3(0 )×2
32-31=3(1 )×2
33-32=3(2 )×2
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立.
(3)计算:3+32+…+32017.
| A. | 24×10-26kg | B. | 2.4×10-25kg | C. | 0.24×10-24kg | D. | 2.4×10-24kg |
