题目内容
13.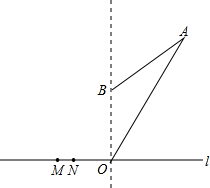 如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)
如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)(1)求该日系船航行的速度.
(2)若该日系船不改变方向继续航行,则其是否会正好行至我国捕鱼船停泊处(即M、N处)?请经过计算说明理由.
分析 (1)过点A作AP⊥OB垂足为P,Rt△APO中,OA=20$\sqrt{3}$km,在Rt△APO中,求出PO=$\sqrt{(20\sqrt{3})^{2}-(10\sqrt{3})^{2}}$=30km,进而求出AB的长,然后求出日系船的航行速度;
(2)延长AB交l于点Q,利用BO=20 km,根据cot∠BQO=$\frac{QO}{PO}$,求出QO的长,再比较即可.
解答 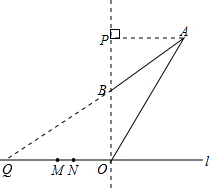 解:(1)过点A作AP⊥OB垂足为P,Rt△APO中,OA=20$\sqrt{3}$km,
解:(1)过点A作AP⊥OB垂足为P,Rt△APO中,OA=20$\sqrt{3}$km,
∵sin∠AOP=$\frac{AP}{AO}$=$\frac{AP}{20\sqrt{3}}$=$\frac{1}{2}$
∴AP=10$\sqrt{3}$km,
Rt△APO中,PO=$\sqrt{(20\sqrt{3})^{2}-(10\sqrt{3})^{2}}$=30km,
∵BO=20 km,
∴BP=10 km,Rt△APB中,AB=$\sqrt{(10\sqrt{3})^{2}+{10}^{2}}$=20km,
∴该日系船航行的速度为:$\frac{20}{\frac{2}{3}}$=30km/h;
(2)延长AB交l于点Q,易求∠BQO=∠PAB=30°,
∵BO=20 km,cot∠BQO=$\frac{QO}{PO}$,
∴QO=20$\sqrt{3}$km>30>29,
日系船不会行至我国捕鱼船停泊处.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )
如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )
 如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )
如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6$\sqrt{3}$cm,那么CE等于( )| A. | 3cm | B. | 2cm | C. | 4cm | D. | $\sqrt{3}$cm |
8.如果点E,F,G,H分别是菱形ABCD四边AB,BC,CD,DA上的中点,那么四边形EFGH是( )
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 以上都不是 |
 如图,在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,求证:AD平分∠FAC.
如图,在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,求证:AD平分∠FAC.