题目内容
8.如果点E,F,G,H分别是菱形ABCD四边AB,BC,CD,DA上的中点,那么四边形EFGH是( )| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 以上都不是 |
分析 如图,作辅助线;首先运用三角形的中位线定理证明四边形EFGH为平行四边形,进而证明∠EFG=90°,即可判断四边形EFGH为矩形.
解答 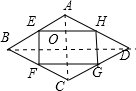 解:如图,连接AC、BD;
解:如图,连接AC、BD;
∵四边形ABCD为菱形,
∴AC⊥BD.而点E,F,G,H分别是菱形ABCD四边的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC;同理可证:FG∥BD,
GH∥AC,GH=$\frac{1}{2}$AC,
∴EF∥GH,EF=GH,
∴四边形EFGH为平行四边形;
∵EF∥AC,FG∥BD,AC⊥BD,
∴∠EFG=90°,
∴四边形EFGH为矩形,
故选B.
点评 该题主要考查了菱形的性质、三角形的中位线定理、矩形的判定等几何知识点及其应用问题;解题的方法是作辅助线;解题的关键是灵活运用三角形的中位线定理、矩形的判定等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
18.9的算术平方根是( )
| A. | 81 | B. | 3 | C. | -3 | D. | ±3 |
16.若关于x的方程2x+a-4=0的解是x=-2,则a的值等于( )
| A. | -8 | B. | 0 | C. | 8 | D. | 2 |
3.|-$\frac{1}{2}$|的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
18.计算3a3÷a2的结果是( )
| A. | 2a | B. | 3a2 | C. | 3a | D. | 3 |
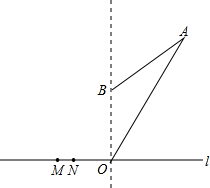 如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)
如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)