解不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1＞0}\\{2-x≥0}\end{array}\right.$．题目和参考答案——青夏教育精英家教网—

题目内容

3．解不等式组$\left\{\begin{array}{l}{\frac{1}{3}x+1＞0}\\{2-x≥0}\end{array}\right.$．

分析首先计算出两个一元一次不等式的解集，再根据大小小大中间找可得不等式组的解集．

解答解：$\left\{\begin{array}{l}{\frac{1}{3}x+1＞0①}\\{2-x≥0②}\end{array}\right.$，
由①得：x＞-3，
由②得：x≤2，
不等式组的解集为：-3＜x≤2．

点评此题主要考查了一元一次不等式组的解法，关键是掌握解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．

练习册系列答案

相关题目

13．

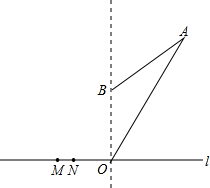如图：我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船，MN=1km，我国海监船在点M的正东方向30km的点O处，观测到一日系船正匀速直线航向我国海域，当该日系船位于点O的北偏东30°方向上的A处（OA=20$\sqrt{3}$km）时，我方开始向日方喊话，但该日系船仍匀速航行，40min后，又测该日系船位于点O的正北方向上的点B处，且OB=20km．（参考数据：$\sqrt{3}$≈1.732）
（1）求该日系船航行的速度．
（2）若该日系船不改变方向继续航行，则其是否会正好行至我国捕鱼船停泊处（即M、N处）？请经过计算说明理由．

14．

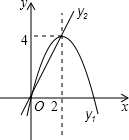如图，已知抛物线y₁=-x²+4x和直线y₂=2x，我们约定：当x任取一值时，x对应的函数值分别为y₁、y₂，若y₁≠y₂，取y₁、y₂中的较小值记为M；若y₁=y₂，记M=y₁=y₂．
下列判断：
①当x＞2时，M=y₂；
②当x＜0时，x值越大，M值越大；
③使得M大于4的x值不存在；
④若M=2，则x=1．
其中正确的有（　　）

11．若分式$\frac{{x}^{2}-4}{x+2}$的值为零，则x的值为（　　）

3a²

8．某果园2012年水果产量为100吨，2014年水果产量为144吨，求该果园水果产量的年平均增长率．设该果园水果产量的年平均增长率为x，则根据题意可列方程为（　　）

15．下列哪一个选项中的等式不成立？（　　）

	A．	$\sqrt{{3}^{8}}$=3⁴		B．	$\sqrt{（-5）^{6}}$=（-5）³
	C．	$\sqrt{{3}^{4}×{5}^{10}}$=3²×5⁵		D．	$\sqrt{（-3）^{4}×（-5）^{8}}$=（-3）²×（-5）⁴

如果∠A的两边分别与∠B的两边平行，且∠A比∠B的3倍少40°，则这两个角的度数分别为______________．

能使有意义的x的取值范围是（）

A. x＞-2 B. x≥-2 C. x≥-2且x≠0 D. x＞0

试题分类