题目内容
15.若|x-y|+(y+1)2=0,则x2+y2的结果是( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 根据非负数的和为零,可得每个非负数为零,根据解不等式组,可得x、y的值,根据有理数的运算,可得答案.
解答 解:由|x-y|+(y+1)2=0,得
$\left\{\begin{array}{l}{x-y=0}\\{y+1=0}\end{array}\right.$.
解得$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$.
x2+y2=(-1)2+(-1)2=2,
故选:A.
点评 本题考查了非负数的性质,利用非负数的和为零得出每个非负数为零是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
5. 如图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
如图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
 如图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
如图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )| A. | 体育场离张强家3.5千米 | |
| B. | 张强在体育场锻炼了15分钟 | |
| C. | 体育场离早餐店1.5千米 | |
| D. | 张强从早餐店回家的平均速度是3千米/小时 |
10.“H7N9”是一种新型禽流感,其病毒颗粒呈多形性,其汇总球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( )
| A. | 1.2×10-9米 | B. | 1.2×10-8米 | C. | 1.2×10-7米 | D. | 12×10-9米 |
7.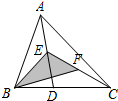 如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
 如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )| A. | 1cm2 | B. | 2cm2 | C. | 8cm2 | D. | 16cm2 |
4.下列计算正确的是( )
| A. | 2m3+3m2=5m5 | B. | -5(-x3)-2=-$\frac{5}{{x}^{6}}$ | C. | (3a3b3)2=6a6b6 | D. | $\sqrt{(-2)^{2}}$=-2 |
5.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式拼接.若用餐的人数有90人,则这样的餐桌需要( )张?


| A. | 15 | B. | 16 | C. | 21 | D. | 22 |
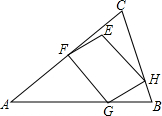 如图,在△ABC中,AB=AC,∠A=36°,?EFGH的顶点F、G、H分别在AC,AB,BC边上,且FC=CH.
如图,在△ABC中,AB=AC,∠A=36°,?EFGH的顶点F、G、H分别在AC,AB,BC边上,且FC=CH.